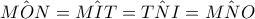και διαμέτρου
και διαμέτρου  . Δεχόμαστε ότι ένα σημείο ,
. Δεχόμαστε ότι ένα σημείο ,  του ημικυκλίου βρίσκεται κοντά στο
του ημικυκλίου βρίσκεται κοντά στο  ,
,έτσι ώστε η μεσοκάθετη στην ακτίνα
 τέμνει την ακτίνα
τέμνει την ακτίνα  σε σημείο
σε σημείο  . Ας είναι και σημείο
. Ας είναι και σημείο  της ακτίνας
της ακτίνας  με ,
με ,  .
.Αν
 τα μέσα των
τα μέσα των  αντίστοιχα , δείξετε ότι :
αντίστοιχα , δείξετε ότι :  .
.Τα μαθηματικά δεν έχουν στεγανά , άρα όλες οι λύσεις «μετράνε».
Όμως λύσεις με ύλη Α λυκείου ή Γ γυμνασίου ( χωρίς τριγωνομετρία ) είναι εντός φακέλου .

 και λόγω της
και λόγω της  οι κόκκινες γωνίες είναι ίσες.
οι κόκκινες γωνίες είναι ίσες.  και
και  Άρα τα τρίγωνα
Άρα τα τρίγωνα 
 θα είναι και
θα είναι και 
 είναι ισοσκελές, οπότε
είναι ισοσκελές, οπότε  . Άρα
. Άρα  και από παραλληλία είναι
και από παραλληλία είναι  . Άρα τα τρίγωνα
. Άρα τα τρίγωνα  είναι όμοια αφού
είναι όμοια αφού  , και
, και  , και έχουν ίσες περιεχόμενες γωνίες. Τώρα, αφού το δεύτερο είναι ισοσκελές, έπεται ότι είναι ισοσκελές και το πρώτο, από όπου το ζητούμενο.
, και έχουν ίσες περιεχόμενες γωνίες. Τώρα, αφού το δεύτερο είναι ισοσκελές, έπεται ότι είναι ισοσκελές και το πρώτο, από όπου το ζητούμενο. του
του 
 μεταφέρεται μέσω ίσων τμημάτων στο γινόμενο
μεταφέρεται μέσω ίσων τμημάτων στο γινόμενο 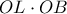
 εγγράψιμο
εγγράψιμο

 μέσω της ισότητας
μέσω της ισότητας 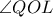
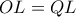
 ,
,
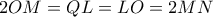
 συμμετρικό του
συμμετρικό του  ως προς
ως προς  οπότε
οπότε  . Θα αποδείξουμε ότι
. Θα αποδείξουμε ότι 
 προφανώς το
προφανώς το  είναι ισοσκελές τραπέζιο,άρα
είναι ισοσκελές τραπέζιο,άρα οπότε
οπότε  μεσοκάθετος της
μεσοκάθετος της  το
το  είναι παραλ/μμο ,άρα και
είναι παραλ/μμο ,άρα και  ,
,  ,
,  είναι εγγράψιμο και
είναι εγγράψιμο και