 και διάμετρο
και διάμετρο  θεωρούμε σημείο
θεωρούμε σημείο  και φέρουμε το ύψος
και φέρουμε το ύψος  του τριγώνου
του τριγώνου  . Η εφαπτομένη
. Η εφαπτομένη  στο σημείο
στο σημείο  του ημικυκλιου τέμνει την εφαπτομένη στο σημείο
του ημικυκλιου τέμνει την εφαπτομένη στο σημείο  του ημικυκλιου στο σημείο
του ημικυκλιου στο σημείο  και οι ευθείες
και οι ευθείες 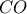 και
και  τέμνονται στο σημείο
τέμνονται στο σημείο  . Η ευθεία
. Η ευθεία  τέμνει την
τέμνει την  στο σημείο
στο σημείο  . Να δείξετε ότι η
. Να δείξετε ότι η  διχοτομεί την
διχοτομεί την  .
.Οι λύσεις είναι ευπρόσδεκτες από όλους τους μαθητές.

 επανατέμνει τον
επανατέμνει τον  στο
στο  και με
και με  την πολική του
την πολική του  το τετράπλευρο
το τετράπλευρο  είναι αρμονικό , άρα με
είναι αρμονικό , άρα με  είναι
είναι 
 εφάπτεται στον κύκλο
εφάπτεται στον κύκλο  άρα
άρα  άρα η δέσμη
άρα η δέσμη  είναι αρμονική και αφού οι ακτίνες της δέσμης τέμνουν την ευθεία
είναι αρμονική και αφού οι ακτίνες της δέσμης τέμνουν την ευθεία  άρα η σημεισοειρά
άρα η σημεισοειρά  είναι αρμονική, άρα και η δέσμη
είναι αρμονική, άρα και η δέσμη  είναι αρμονική και αφού η
είναι αρμονική και αφού η  εφάπτεται στον κύκλο
εφάπτεται στον κύκλο 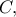 παίρνουμε
παίρνουμε  άρα η ευθεία
άρα η ευθεία 
 Με
Με  από Θ. Μενέλαου στο τρίγωνο
από Θ. Μενέλαου στο τρίγωνο  με διατέμνουσα
με διατέμνουσα  παίρνουμε
παίρνουμε 
 και από Θ. Μενέλαου στο τρίγωνο
και από Θ. Μενέλαου στο τρίγωνο  με διατέμνουσα
με διατέμνουσα  παίρνουμε
παίρνουμε 
 με διατέμνουσα
με διατέμνουσα  είναι
είναι  Επομένως, είναι
Επομένως, είναι  Αφού
Αφού 

 με τέμνουσα
με τέμνουσα  παίρνουμε
παίρνουμε 




![\overset{(6)}\Longrightarrow CX^{2}=\frac{\displaystyle CB\cdot CO \left [\left ( CO+\frac{AB^{2}-2AC^{2}}{AB} \right )\left ( AC\cdot CB+\frac{AB^{2}-2AC^{2}}{AB}\cdot \frac{CB\cdot CO}{AC} \right )-2CO \cdot EB \cdot OD\right ]}{\displaystyle AC\left ( CO+2OD \right )^{2}}\left ( 7 \right ). \overset{(6)}\Longrightarrow CX^{2}=\frac{\displaystyle CB\cdot CO \left [\left ( CO+\frac{AB^{2}-2AC^{2}}{AB} \right )\left ( AC\cdot CB+\frac{AB^{2}-2AC^{2}}{AB}\cdot \frac{CB\cdot CO}{AC} \right )-2CO \cdot EB \cdot OD\right ]}{\displaystyle AC\left ( CO+2OD \right )^{2}}\left ( 7 \right ).](/forum/ext/geomar/texintegr/latexrender/pictures/b917da4cd5b0803f0343f36c1b5f9648.png)

![\displaystyle \overset{(7)}=\frac{\displaystyle CB^{4}\cdot CO^{2}}{\displaystyle CB\cdot CO\left[\left (CO+\frac{AB^{2}-2AC^{2}}{AB} \right )\left ( AC^{2}\cdot CB+\frac{\left ( AB^{2}-2AC^{2} \right )\cdot CB\cdot CO}{AB} \right )-\frac{AC \cdot EC \left ( AB^{2}-2AC^{2} \right )}{2} \right]}= \displaystyle \overset{(7)}=\frac{\displaystyle CB^{4}\cdot CO^{2}}{\displaystyle CB\cdot CO\left[\left (CO+\frac{AB^{2}-2AC^{2}}{AB} \right )\left ( AC^{2}\cdot CB+\frac{\left ( AB^{2}-2AC^{2} \right )\cdot CB\cdot CO}{AB} \right )-\frac{AC \cdot EC \left ( AB^{2}-2AC^{2} \right )}{2} \right]}=](/forum/ext/geomar/texintegr/latexrender/pictures/511d0d38970b0bf8f3186d4611d74792.png)
![\displaystyle \overset{\angle ACB=90^{\circ}}=\frac{\displaystyle CB^{3}\cdot CO}{\displaystyle \left [ \left ( CO+\frac{2CB^{2}-AB^{2}}{AB} \right )\left ( \left ( AB^{2}-CB^{2} \right )\cdot CB+\frac{1}{2}\left ( 2CB^{2}-AB^{2} \right )\cdot CB \right )-\frac{1}{2}CB\cdot CO\left ( 2CB^{2}-AB^{2} \right )\right]}= \displaystyle \overset{\angle ACB=90^{\circ}}=\frac{\displaystyle CB^{3}\cdot CO}{\displaystyle \left [ \left ( CO+\frac{2CB^{2}-AB^{2}}{AB} \right )\left ( \left ( AB^{2}-CB^{2} \right )\cdot CB+\frac{1}{2}\left ( 2CB^{2}-AB^{2} \right )\cdot CB \right )-\frac{1}{2}CB\cdot CO\left ( 2CB^{2}-AB^{2} \right )\right]}=](/forum/ext/geomar/texintegr/latexrender/pictures/e2e242ff02a2ff391d793f877ca572bb.png)

 διχοτόμος της γωνίας
διχοτόμος της γωνίας