![f \colon [\alpha,\beta] \to \mathbb{R} f \colon [\alpha,\beta] \to \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/24e2e8b445357991ff58c01c1f8d32f6.png)
με συνεχή πρώτη παράγωγο και

Να αποδειχθεί ότι υπάρχουν
![\gamma,\delta\in[\alpha,\beta] \gamma,\delta\in[\alpha,\beta]](/forum/ext/geomar/texintegr/latexrender/pictures/0a39dfaf8beb0138b29aa9b2fcc184c9.png) τέτοια ώστε
τέτοια ώστε  και
και 
ΣΗΜΕΙΩΣΗ
Η εκφώνηση είναι πλήρης, το σχήμα είναι ενδεικτικό.
Συντονιστής: emouroukos
![f \colon [\alpha,\beta] \to \mathbb{R} f \colon [\alpha,\beta] \to \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/24e2e8b445357991ff58c01c1f8d32f6.png)

![\gamma,\delta\in[\alpha,\beta] \gamma,\delta\in[\alpha,\beta]](/forum/ext/geomar/texintegr/latexrender/pictures/0a39dfaf8beb0138b29aa9b2fcc184c9.png) τέτοια ώστε
τέτοια ώστε  και
και 


 αρα
αρα  γν.φθίνουσα στο
γν.φθίνουσα στο ![\displaystyle{[a,b]} \displaystyle{[a,b]}](/forum/ext/geomar/texintegr/latexrender/pictures/14f53999651f504e8f7c5c1b74530f3e.png)
 δεν είναι σταθερή
δεν είναι σταθερή με
με  φέρουμε //στο τμήμα
φέρουμε //στο τμήμα ![\displaystyle{[a,b]} \displaystyle{[a,b]}](/forum/ext/geomar/texintegr/latexrender/pictures/14f53999651f504e8f7c5c1b74530f3e.png) αυτή θα τμήση την
αυτή θα τμήση την  σε κάποιο σημείο
σε κάποιο σημείο  με
με  αφού σύνολο τιμών της
αφού σύνολο τιμών της  όταν}
όταν} είναι ιδιο όταν
είναι ιδιο όταν  kαι είναι το
kαι είναι το ![\displaystyle{[m,0] \displaystyle{[m,0]](/forum/ext/geomar/texintegr/latexrender/pictures/d49e084640ae0f7acdffa3b5175b055a.png) \displaystyle{
\displaystyle{ \displaystyle{
\displaystyle{ \displaystyle{ αφου }
\displaystyle{ αφου } \displaystyle{ γν.φθίνουσα με }
\displaystyle{ γν.φθίνουσα με } \displaystyle{ για οποιαδήποτε
\displaystyle{ για οποιαδήποτε  που ορίστηκαν όπως πριν
που ορίστηκαν όπως πριν των κρίσιμων σημείων της
των κρίσιμων σημείων της  . Έχω
. Έχω ![f'(\xi_\nu)=0,\xi_\nu\in[\alpha,\beta],\nu\in N^*,\xi_0=\alpha f'(\xi_\nu)=0,\xi_\nu\in[\alpha,\beta],\nu\in N^*,\xi_0=\alpha](/forum/ext/geomar/texintegr/latexrender/pictures/7da4285edb52aa58f2905d76ebc47b64.png) .
. είναι συνεχής στο κλειστό διάστημα
είναι συνεχής στο κλειστό διάστημα ![[\alpha,\beta] [\alpha,\beta]](/forum/ext/geomar/texintegr/latexrender/pictures/76ec9b92b11ea1475095ec6a47fccd53.png) . Από το θεώρημα μέγιστης τιμής, υπάρχει
. Από το θεώρημα μέγιστης τιμής, υπάρχει ![x_0\in[\alpha,\beta] x_0\in[\alpha,\beta]](/forum/ext/geomar/texintegr/latexrender/pictures/8369f0bc54dfd29bc97e1e8b07d493db.png) τέτοιο, ώστε
τέτοιο, ώστε ![f(x_0)=M=maxf([\alpha,\beta]) f(x_0)=M=maxf([\alpha,\beta])](/forum/ext/geomar/texintegr/latexrender/pictures/5c31e519ee14224175f0566b43e3034a.png) . Οπότε
. Οπότε  και έστω
και έστω  για κάποιο
για κάποιο  .
. . Αν δεν υπάρχει το
. Αν δεν υπάρχει το  θέτω
θέτω  .
. η συνεχής συνάρτηση
η συνεχής συνάρτηση  διατηρεί το πρόσημό της, άρα η
διατηρεί το πρόσημό της, άρα η  είναι γνησίως μονότονη στο διάστημα αυτό και αφού
είναι γνησίως μονότονη στο διάστημα αυτό και αφού  , η
, η  είναι γνησίως αύξουσα άρα
είναι γνησίως αύξουσα άρα  για κάθε
για κάθε  .
Με όμοιο τρόπο δείχνω ότι
.
Με όμοιο τρόπο δείχνω ότι 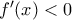 για κάθε
για κάθε  . (Αν δεν υπάρχει το
. (Αν δεν υπάρχει το  θέτω
θέτω  .)
.)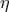 τέτοιο ώστε
τέτοιο ώστε  . Από το θεώρημα ενδιάμεσων τιμών υπάρχουν
. Από το θεώρημα ενδιάμεσων τιμών υπάρχουν  τέτοια ώστε
τέτοια ώστε  . Από τα προηγούμενα έχω επιπλέον ότι
. Από τα προηγούμενα έχω επιπλέον ότι  άρα
άρα  , όπως θέλαμε.
, όπως θέλαμε. τότε παίρνω το
τότε παίρνω το  με
με ![f(x_0)=m=minf[\alpha,\beta] f(x_0)=m=minf[\alpha,\beta]](/forum/ext/geomar/texintegr/latexrender/pictures/e942fc5bf61b9f272a8add7964f8048c.png) και δουλεύω όπως πριν. (Εδώ οι μονοτονίες αλλάζουν όπως και τα πρόσημα των παραγώγων).
και δουλεύω όπως πριν. (Εδώ οι μονοτονίες αλλάζουν όπως και τα πρόσημα των παραγώγων). να προκύπτει σε υποδιάστημα που η συνάρτηση είναι σταθερή. Δηλαδή
να προκύπτει σε υποδιάστημα που η συνάρτηση είναι σταθερή. Δηλαδή ![\xi_\kappa\in (c,d)\subset[\alpha,\beta] , f(x)=f(\xi_\kappa)=M \ \forall x\in (c,d) \xi_\kappa\in (c,d)\subset[\alpha,\beta] , f(x)=f(\xi_\kappa)=M \ \forall x\in (c,d)](/forum/ext/geomar/texintegr/latexrender/pictures/97a5a618096291572ea782a8349468a3.png) .
Θεωρούμε τα σύνολα
.
Θεωρούμε τα σύνολα  και
και  . Αν
. Αν  , τότε θέτω
, τότε θέτω  , αλλιώς θέτω
, αλλιώς θέτω  . Όμοια αν
. Όμοια αν  , τότε θέτω
, τότε θέτω  , αλλιώς θέτω
, αλλιώς θέτω  . Προφανώς υπάρχει
. Προφανώς υπάρχει 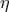 τέτοιο ώστε
τέτοιο ώστε  και συνεχίζω κατά τα γνωστά.
και συνεχίζω κατά τα γνωστά.Όμως ηadd2math έγραψε: ↑Πέμ Μάιος 08, 2025 9:13 pmΈστω η γνησίως αύξουσα ακολουθίατων κρίσιμων σημείων της
. Έχω
.
Ηείναι συνεχής στο κλειστό διάστημα
. Από το θεώρημα μέγιστης τιμής, υπάρχει
τέτοιο, ώστε
. Οπότε
και έστω
για κάποιο
.
Θέτω. Αν δεν υπάρχει το
θέτω
.
Στο διάστημαη συνεχής συνάρτηση
διατηρεί το πρόσημό της, άρα η
είναι γνησίως μονότονη στο διάστημα αυτό και αφού
, η
είναι γνησίως αύξουσα άρα
για κάθε
.
κατιευλογο4.png
Με όμοιο τρόπο δείχνω ότιγια κάθε
. (Αν δεν υπάρχει το
θέτω
.)
Προφανώς υπάρχειτέτοιο ώστε
. Από το θεώρημα ενδιάμεσων τιμών υπάρχουν
τέτοια ώστε
. Από τα προηγούμενα έχω επιπλέον ότι
άρα
, όπως θέλαμε.
Αντότε παίρνω το
με
και δουλεύω όπως πριν. (Εδώ οι μονοτονίες αλλάζουν όπως και τα πρόσημα των παραγώγων).
Άλλη περίπτωση είναι το ολικό μέγιστονα προκύπτει σε υποδιάστημα που η συνάρτηση είναι σταθερή. Δηλαδή
. κατιευλογο4b.png
Θεωρούμε τα σύνολακαι
. Αν
, τότε θέτω
, αλλιώς θέτω
. Όμοια αν
, τότε θέτω
, αλλιώς θέτω
. Προφανώς υπάρχει
τέτοιο ώστε
και συνεχίζω κατά τα γνωστά.
 μπορεί να είναι τέτοια ώστε
μπορεί να είναι τέτοια ώστε 

![[\alpha,\beta] [\alpha,\beta]](/forum/ext/geomar/texintegr/latexrender/pictures/76ec9b92b11ea1475095ec6a47fccd53.png) με
με  )
) 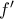 και από τα δεξιά και από τα αριστερά του
και από τα δεξιά και από τα αριστερά του  να λαμβάνει και θετικές και αρνητικές τιμές οπότε σε κανένα διάστημα με άκρο το
να λαμβάνει και θετικές και αρνητικές τιμές οπότε σε κανένα διάστημα με άκρο το  η
η  να μην είναι μονότονη. Σε αυτή την περίπτωση το παραπάνω επιχείρημα δεν επαρκεί.
να μην είναι μονότονη. Σε αυτή την περίπτωση το παραπάνω επιχείρημα δεν επαρκεί.ενδιαφέρουσα λύση, ευχαριστώ πολύ για τις πληροφορίες, θα προσπαθήσω όπως έγραψεςadd2math έγραψε: ↑Πέμ Μάιος 08, 2025 9:13 pmΈστω η γνησίως αύξουσα ακολουθίατων κρίσιμων σημείων της
. Έχω
.
Ηείναι συνεχής στο κλειστό διάστημα
. Από το θεώρημα μέγιστης τιμής, υπάρχει
τέτοιο, ώστε
. Οπότε
και έστω
για κάποιο
.
Θέτω. Αν δεν υπάρχει το
θέτω
.
Στο διάστημαη συνεχής συνάρτηση
διατηρεί το πρόσημό της, άρα η
είναι γνησίως μονότονη στο διάστημα αυτό και αφού
Verde Casino, η
είναι γνησίως αύξουσα άρα
για κάθε
.
κατιευλογο4.png
Με όμοιο τρόπο δείχνω ότιγια κάθε
. (Αν δεν υπάρχει το
θέτω
.)
Προφανώς υπάρχειτέτοιο ώστε
. Από το θεώρημα ενδιάμεσων τιμών υπάρχουν
τέτοια ώστε
. Από τα προηγούμενα έχω επιπλέον ότι
άρα
, όπως θέλαμε.
Αντότε παίρνω το
με
και δουλεύω όπως πριν. (Εδώ οι μονοτονίες αλλάζουν όπως και τα πρόσημα των παραγώγων).
Άλλη περίπτωση είναι το ολικό μέγιστονα προκύπτει σε υποδιάστημα που η συνάρτηση είναι σταθερή. Δηλαδή
. κατιευλογο4b.png
Θεωρούμε τα σύνολακαι
. Αν
, τότε θέτω
, αλλιώς θέτω
. Όμοια αν
, τότε θέτω
, αλλιώς θέτω
. Προφανώς υπάρχει
τέτοιο ώστε
και συνεχίζω κατά τα γνωστά.
 με συνεχή πρώτη παράγωγο, το πρόσημο της πρώτης παραγώγου δεν αλλάζει ανάμεσα σε δυο διαδοχικά εσωτερικά κρίσιμα σημεία.
με συνεχή πρώτη παράγωγο, το πρόσημο της πρώτης παραγώγου δεν αλλάζει ανάμεσα σε δυο διαδοχικά εσωτερικά κρίσιμα σημεία. που όμως δεν είναι συνεχής στο
που όμως δεν είναι συνεχής στο  .
. , όπως βλέπουμε παρακάτω, μπορούμε πάντα για κάθε ολικό μέγιστο (με τετμημένη
, όπως βλέπουμε παρακάτω, μπορούμε πάντα για κάθε ολικό μέγιστο (με τετμημένη  ) να έχουμε στα αριστερά του ένα άλλο κρίσιμο σημείο (το προηγούμενο με τετμημένη
) να έχουμε στα αριστερά του ένα άλλο κρίσιμο σημείο (το προηγούμενο με τετμημένη  ), όσο στριμωγμένα και να είναι αυτά τα σημεία. Στο διάστημα
), όσο στριμωγμένα και να είναι αυτά τα σημεία. Στο διάστημα  η συνεχής
η συνεχής  διατηρεί το πρόσημό της και επομένως η
διατηρεί το πρόσημό της και επομένως η  δεν αλλάζει μονοτονία.
.
δεν αλλάζει μονοτονία.
.Η ένστασή μου παραμένει αν και ομολογώ πως θα μπορούσε να είχε διατυπωθεί αναλυτικότερα:add2math έγραψε: ↑Τρί Μάιος 13, 2025 8:41 pmΤο επιχείρημά μου βασίζεται στην παρακάτω πρόταση (που είναι άμεση).
Για μη σταθερή παραγωγίσιμη συνάρτησημε συνεχή πρώτη παράγωγο, το πρόσημο της πρώτης παραγώγου δεν αλλάζει ανάμεσα σε δυο διαδοχικά εσωτερικά κρίσιμα σημεία.
Μια συνάρτηση που ίσως υπονοεί ο Ιάσωνας είναι ηπου όμως δεν είναι συνεχής στο
.
Ακόμα κι αν πάρουμε έναν κατάλληλο περιορισμό της, όπως βλέπουμε παρακάτω, μπορούμε πάντα για κάθε ολικό μέγιστο (με τετμημένη
) να έχουμε στα αριστερά του ένα άλλο κρίσιμο σημείο (το προηγούμενο με τετμημένη
), όσο στριμωγμένα και να είναι αυτά τα σημεία. Στο διάστημα
η συνεχής
διατηρεί το πρόσημό της και επομένως η
δεν αλλάζει μονοτονία.
evlogo4b.png.
Αν υπάρχει κάτι άλλο που δεν βλέπω, με χαρά να το ξαναδούμε.
 είτε θα υπάρχει ένα κρίσιμο σημείο
είτε θα υπάρχει ένα κρίσιμο σημείο  ώστε η
ώστε η 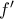 να είναι για κάποιο
να είναι για κάποιο  θετική σε ένα εκ των διαστημάτων
θετική σε ένα εκ των διαστημάτων  ,
,  και αρνητική στο άλλο
και αρνητική στο άλλο είτε θα υπάρχει διάστημα
είτε θα υπάρχει διάστημα ![[c,d] [c,d]](/forum/ext/geomar/texintegr/latexrender/pictures/c31d2b7df15fa7d119c2f8d13f69e10b.png) στο οποίο η
στο οποίο η  θα είναι σταθερή, η
θα είναι σταθερή, η 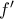 θα διατηρεί πρόσημο σε κάποιο διάστημα
θα διατηρεί πρόσημο σε κάποιο διάστημα  ενώ σε κάποιο διάστημα
ενώ σε κάποιο διάστημα  πάλι θα διατηρεί πρόσημο αλλά θα είναι αντίθετο από το πρόσημο στο
πάλι θα διατηρεί πρόσημο αλλά θα είναι αντίθετο από το πρόσημο στο  .
. εντάσσεται σε αυτές τις περιπτώσεις όντως καταλήγουμε στο ζητούμενο, αφού έχουμε τη δυνατότητα να αγνοήσουμε ενδεχόμενα παθολογικά κρίσιμα σημεία μετατοπίζοντας την προσοχή μας προς κάποιο που να εξυπηρετεί όπως εξηγείτε στη δευτερολογία σας κατά την πραγμάτευση της
εντάσσεται σε αυτές τις περιπτώσεις όντως καταλήγουμε στο ζητούμενο, αφού έχουμε τη δυνατότητα να αγνοήσουμε ενδεχόμενα παθολογικά κρίσιμα σημεία μετατοπίζοντας την προσοχή μας προς κάποιο που να εξυπηρετεί όπως εξηγείτε στη δευτερολογία σας κατά την πραγμάτευση της 
 το πλήθος των κρισίμων σημείων της να είναι υπεραριθμήσιμο (οπότε τα κρίσιμα σημεία είναι αδύνατον να αναπαρασταθούν ως όροι ακολουθίας
το πλήθος των κρισίμων σημείων της να είναι υπεραριθμήσιμο (οπότε τα κρίσιμα σημεία είναι αδύνατον να αναπαρασταθούν ως όροι ακολουθίας  )
) Να μην είναι σταθερή σε κανένα διάστημα υποσύνολο του πεδίου ορισμού της
Να μην είναι σταθερή σε κανένα διάστημα υποσύνολο του πεδίου ορισμού της  Για κάθε κρίσιμο σημείο
Για κάθε κρίσιμο σημείο  αυτής να ισχύει τουλάχιστον ένα από τα δυο ακόλουθα:
αυτής να ισχύει τουλάχιστον ένα από τα δυο ακόλουθα: η
η 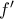 λαμβάνει και θετικές και αρνητικές τιμές στο
λαμβάνει και θετικές και αρνητικές τιμές στο 
 η
η 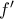 λαμβάνει και θετικές και αρνητικές τιμές στο
λαμβάνει και θετικές και αρνητικές τιμές στο 
 Για όλα τα κρίσιμα σημεία, με την εξαίρεση αριθμησίμου πλήθους, να ισχύουν και τα δύο προαναφερθέντα (δεν είναι σημαντικό αυτό, αλλά αναδεικνύει πόσο εξωτική μπορεί να είναι η εν λόγω συνάρτηση).
Για όλα τα κρίσιμα σημεία, με την εξαίρεση αριθμησίμου πλήθους, να ισχύουν και τα δύο προαναφερθέντα (δεν είναι σημαντικό αυτό, αλλά αναδεικνύει πόσο εξωτική μπορεί να είναι η εν λόγω συνάρτηση). αυτής της συνάρτησης, η παράγωγός της, είτε από δεξιά, είτε από αριστερά, είτε και από τις δυο κατευθύνσεις θα συμπεριφέρεται ως προς το πρόσημο με τρόπο που θα θυμίζει τη συνάρτηση
αυτής της συνάρτησης, η παράγωγός της, είτε από δεξιά, είτε από αριστερά, είτε και από τις δυο κατευθύνσεις θα συμπεριφέρεται ως προς το πρόσημο με τρόπο που θα θυμίζει τη συνάρτηση  κοντά στο
κοντά στο 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης