Έστω
 ένας μεταθετικός δακτύλιος με μονάδα και
ένας μεταθετικός δακτύλιος με μονάδα και  ένα
ένα  -module.
-module. Αν
 είναι ελεύθερο
είναι ελεύθερο  -module με rank
-module με rank  , πώς μπορούμε να δείξουμε ότι
, πώς μπορούμε να δείξουμε ότι 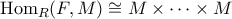 (
( φορές) ;
φορές) ; Μπορείτε να μου δώσετε μία ιδέα;
Συντονιστής: Demetres
 ένας μεταθετικός δακτύλιος με μονάδα και
ένας μεταθετικός δακτύλιος με μονάδα και  ένα
ένα  -module.
-module.  είναι ελεύθερο
είναι ελεύθερο  -module με rank
-module με rank  , πώς μπορούμε να δείξουμε ότι
, πώς μπορούμε να δείξουμε ότι 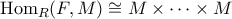 (
( φορές) ;
φορές) ; 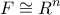 ως
ως  - πρότυπα. Άρα,
- πρότυπα. Άρα, , έχουμε ισομορφισμούς
, έχουμε ισομορφισμούς  - προτύπων
- προτύπων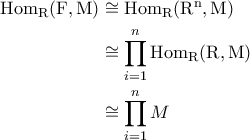
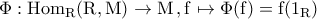
 - προτύπων.
- προτύπων.BAGGP93 έγραψε:η απεικόνιση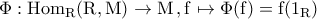
είναι ισομορφισμός- προτύπων.
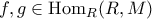 .
. 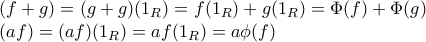
 είναι ομομορφισμός.
είναι ομομορφισμός. 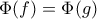 . Τότε
. Τότε 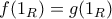 .
. 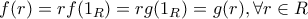 .
.  είναι 1-1.
είναι 1-1.  ορίζουμε την
ορίζουμε την  ως εξής:
ως εξής: 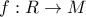 με
με 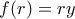
 έχουμε ότι
έχουμε ότι 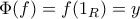 .
.  είναι επί.
είναι επί.BAGGP93 έγραψε:Έχουμε ότιως
- πρότυπα. Άρα,
λόγω μεταθετικότητας του, έχουμε ισομορφισμούς
- προτύπων
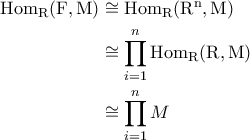
 ;
;Εδώ πολύ σωστά. Μόνο, που στην προτελευταία γραμμή, σβήσε το για κάθεΕιρήνη 33 έγραψε:BAGGP93 έγραψε:η απεικόνιση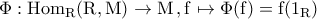
είναι ισομορφισμός- προτύπων.
Για να δείξουμε ότι η απεικόνιση αυτή είναι ισομορφισμός κάνουμε τα εξής;
Έστω.
Έχουμε ότι
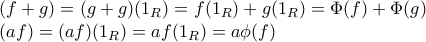
Άρα ηείναι ομομορφισμός.
Έστω. Τότε
.
Άρα.
Άρα ηείναι 1-1.
Για κάθεορίζουμε την
ως εξής:
με
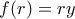
Άρα για κάθεέχουμε ότι
.
Οπότε ηείναι επί.
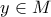 . Όπως έγραψες, αν σου δώσουν
. Όπως έγραψες, αν σου δώσουν 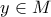 ,
,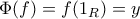 .
.ΑνΕιρήνη 33 έγραψε:BAGGP93 έγραψε:Έχουμε ότιως
- πρότυπα. Άρα,
λόγω μεταθετικότητας του, έχουμε ισομορφισμούς
- προτύπων
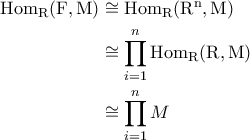
Σε ποιό σημείο χρησιμοποιούμε την μεταθετικότητα του;
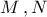 είναι δύο
είναι δύο  - πρότυπα, τότε το σύνολο
- πρότυπα, τότε το σύνολο 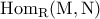 εφοδιασμένο
εφοδιασμένο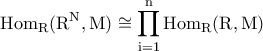 είναι σε επίπεδο αβελιανών ομάδων.
είναι σε επίπεδο αβελιανών ομάδων.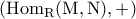 ένα
ένα  - πρότυπο, τότε η φυσιολογική
- πρότυπο, τότε η φυσιολογική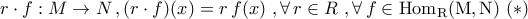
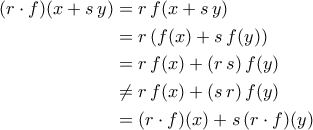 .
. είναι καλώς ορισμένη και με αυτή παίρνουμε
είναι καλώς ορισμένη και με αυτή παίρνουμε  - πρότυπο.
- πρότυπο.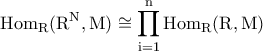 είναι ο
είναι ο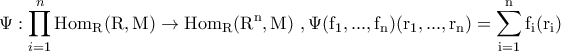 .
.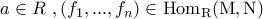 ,
,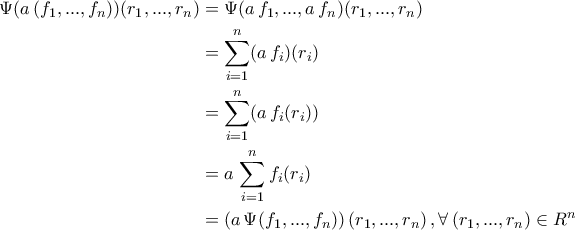
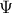 είναι ισομορφισμός
είναι ισομορφισμός  - προτύπων και συνεπώς,
- προτύπων και συνεπώς,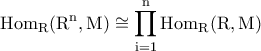 ως
ως  πρότυπα.
πρότυπα.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης