Πάνω από 250 εξαιρετικής αισθητικής ασκήσεις σε εμβαδά στο X (πρώην twitter) εδώ. Χωρίς λύσεις αλλά είναι σχετικά προσιτές, αν και συχνά πονηρές.
Όταν μπείτε στην ιστοσελίδα αυτή μην αμελήσετε να κατεβάσετε το αρχείο PowerPoint που η συγγραφέας έχει συγκεντρώσει τις περισσότερες από τις εν λόγω ασκήσεις. Βάζω το λινκ, έτσι και αλλιώς, εδώ.
Δείγμα η παρακάτω άσκηση. Δίνεται ένα τεταρτοκύκλιο. Μπορείτε να θεωρήσεται ότι το δοθέν κόκκινο σχήμα είναι τετράγωνο με εμβαδόν
 αντί για
αντί για  που δείχνει η εικόνα. Πόσο είναι το κίτρινο εμβαδόν;
που δείχνει η εικόνα. Πόσο είναι το κίτρινο εμβαδόν; Βρήκα ότι η απάντηση αρκετά απρόσμενη. Έχω λύση λίγων γραμμών αλλά θα χαιρόμουν να έβλεπα και άλλες λύσεις.
. Edit. Έκανα διορθώσεις στην αρχική διατύπωση.

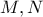 μέσα των πλευρών του , το μεγάλο τετράγωνο έχει εμβαδόν
μέσα των πλευρών του , το μεγάλο τετράγωνο έχει εμβαδόν 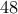 και πλευρά
και πλευρά 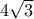 και
και  , δηλαδή εμβαδόν
, δηλαδή εμβαδόν  , οπότε το κίτρινο εμβαδόν ισούται με
, οπότε το κίτρινο εμβαδόν ισούται με  είναι τα μέσα των πλευρών του. Φαίνονται με το μάτι στο σχήμα σαν να είναι μέσα, αλλά δεν τα λαμβάνουμε ως τέτοια. Το αποτέλεσμα ισχύει και χωρίς την υπόθεση ότι είναι μέσα.
είναι τα μέσα των πλευρών του. Φαίνονται με το μάτι στο σχήμα σαν να είναι μέσα, αλλά δεν τα λαμβάνουμε ως τέτοια. Το αποτέλεσμα ισχύει και χωρίς την υπόθεση ότι είναι μέσα. και λόγω συμμετρίας έχω :
και λόγω συμμετρίας έχω :  .
. που ισχύει γιατί εκφράζει το Π. Θ. σε ορθογώνιο τρίγωνο
που ισχύει γιατί εκφράζει το Π. Θ. σε ορθογώνιο τρίγωνο και υποτείνουσα
και υποτείνουσα  που προφανώς ισχύει .
που προφανώς ισχύει . γράφουμε ένα τεταρτοκύκλιο, ένα ημικύκλιο και μία διαγώνιο, όπως στην εικόνα. Πόσο είναι το γραμμοσκιασμένο εμβαδόν; (Από παλιό διαγωνισμό Καγκουρό, για μαθητές Β' και Γ' Λυκείου)
γράφουμε ένα τεταρτοκύκλιο, ένα ημικύκλιο και μία διαγώνιο, όπως στην εικόνα. Πόσο είναι το γραμμοσκιασμένο εμβαδόν; (Από παλιό διαγωνισμό Καγκουρό, για μαθητές Β' και Γ' Λυκείου) .
. είναι τα μέσα δύο απέναντι πλευρών ενός τετραπλεύρου. Δείξτε την ισότητα των εμβαδών
είναι τα μέσα δύο απέναντι πλευρών ενός τετραπλεύρου. Δείξτε την ισότητα των εμβαδών  .
. είναι διάμεσοι τριγώνων οπότε ισχύουν οι ισότητες εμβαδών που αναφέρονται κάτω από το σχήμα.
είναι διάμεσοι τριγώνων οπότε ισχύουν οι ισότητες εμβαδών που αναφέρονται κάτω από το σχήμα. (Στο σχήμα,αντί των
(Στο σχήμα,αντί των 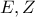 )
) είναι διάμεσοι των τριγώνων
είναι διάμεσοι των τριγώνων  θα είναι
θα είναι![2[(EMK)+(MZK)]=S\Rightarrow (MEKZ)= \dfrac{S}{2} 2[(EMK)+(MZK)]=S\Rightarrow (MEKZ)= \dfrac{S}{2}](/forum/ext/geomar/texintegr/latexrender/pictures/1ec0239603ee3e775dd18196bdca2be9.png) και όμοια
και όμοια 
 οπότε αρκεί να δείξουμε ότι
οπότε αρκεί να δείξουμε ότι 
 .
.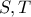 φέρνουμε τις κάθετες επί των
φέρνουμε τις κάθετες επί των  κι από το
κι από το  την κάθετη προς τις
την κάθετη προς τις 
 το
το  είναι τετράγωνο
είναι τετράγωνο  οπότε
οπότε 
