 την εξίσωση
την εξίσωση 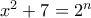
Συντονιστής: nkatsipis

 , οπότε από την αρχική εξίσωση παίρνουμε την παρακάτω:
, οπότε από την αρχική εξίσωση παίρνουμε την παρακάτω: , προφανώς το
, προφανώς το  πρέπει να είναι περιττός.
πρέπει να είναι περιττός. , μετά από τις πράξεις καταλήγουμε ότι:
, μετά από τις πράξεις καταλήγουμε ότι: , Triangular Mersenne numbers
, Triangular Mersenne numbers ,
,  να επιστρέφει το πλήθος των ψηφίων της δυαδικής αναπαράστασης της εισόδου.
να επιστρέφει το πλήθος των ψηφίων της δυαδικής αναπαράστασης της εισόδου.
 είναι άρτιος, τότε
είναι άρτιος, τότε  , οπότε
, οπότε  .
.
 συστήματα κάθε περίπτωσης, γίνεται να αποτιμηθεί ο αριθμός
συστήματα κάθε περίπτωσης, γίνεται να αποτιμηθεί ο αριθμός  .
.
 είναι άρτιος, τότε
είναι άρτιος, τότε 
 είναι περιττός, τότε
είναι περιττός, τότε 
 είναι περιττός, τότε
είναι περιττός, τότε  , οπότε
, οπότε  .
.
 συστήματα κάθε περίπτωσης, γίνεται να αποτιμηθεί ο αριθμός
συστήματα κάθε περίπτωσης, γίνεται να αποτιμηθεί ο αριθμός  .
.
 είναι άρτιος, τότε
είναι άρτιος, τότε 
 είναι περιττός, τότε
είναι περιττός, τότε 
 έτσι, ώστε να λάβουμε την μορφή που θα έχει ο αριθμός
έτσι, ώστε να λάβουμε την μορφή που θα έχει ο αριθμός  σε κάθε περίπτωση;
σε κάθε περίπτωση;Nikitas K. έγραψε: ↑Δευ Απρ 22, 2024 4:00 pm,
Έστω, η συνάρτησηνα επιστρέφει το πλήθος των ψηφίων της δυαδικής αναπαράστασης της εισόδου.
- Αν
είναι άρτιος, τότε
, οπότε
.
Θέτω,
Επιλύοντας τασυστήματα κάθε περίπτωσης, γίνεται να αποτιμηθεί ο αριθμός
.
- Αν
είναι άρτιος, τότε
- Αν
είναι περιττός, τότε
- Αν
είναι περιττός, τότε
, οπότε
.
Θέτω,
Επιλύοντας τασυστήματα κάθε περίπτωσης, γίνεται να αποτιμηθεί ο αριθμός
.
- Αν
είναι άρτιος, τότε
- Αν
είναι περιττός, τότε
Δεν είμαι σίγουρος ότι βγαίνει έτσι αυτή η διοφαντική.Nikitas K. έγραψε: ↑Σάβ Απρ 27, 2024 12:07 pmΧαίρετε,
Έχοντας φτάσει ως το παρακάτω σημείο, υπάρχει κάποιος τρόπος να συνεχίστεί ο υπολογισμός όλων των δυαδικών ψηφίων του αριθμούέτσι, ώστε να λάβουμε την μορφή που θα έχει ο αριθμός
σε κάθε περίπτωση;
Nikitas K. έγραψε: ↑Δευ Απρ 22, 2024 4:00 pm,
Έστω, η συνάρτησηνα επιστρέφει το πλήθος των ψηφίων της δυαδικής αναπαράστασης της εισόδου.
- Αν
είναι άρτιος, τότε
, οπότε
.
Θέτω,
Επιλύοντας τασυστήματα κάθε περίπτωσης, γίνεται να αποτιμηθεί ο αριθμός
.
- Αν
είναι άρτιος, τότε
- Αν
είναι περιττός, τότε
- Αν
είναι περιττός, τότε
, οπότε
.
Θέτω,
Επιλύοντας τασυστήματα κάθε περίπτωσης, γίνεται να αποτιμηθεί ο αριθμός
.
- Αν
είναι άρτιος, τότε
- Αν
είναι περιττός, τότε
Ας γράψω τι σκέφτηκα, αλλα δεν έχω και πολύ χρόνο να το αναλύσω, το αφήνω ως ιδέα μήπως προχωρήσει κάπως.
 άρτιο είναι σχετικά απλό (διαφορά τετραγώνων).
άρτιο είναι σχετικά απλό (διαφορά τετραγώνων). περιττό έχουμε:
περιττό έχουμε:
 , τότε απλά τη γράφουμε στη μορφή:
, τότε απλά τη γράφουμε στη μορφή: , σαφώς με τις κατάλληλες υποθέσεις.
, σαφώς με τις κατάλληλες υποθέσεις. , μία ας τη θεωρήσουμε πρωταρχική λύση των εξισώσεων
, μία ας τη θεωρήσουμε πρωταρχική λύση των εξισώσεων  .
. έχει λύση
έχει λύση 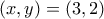

 . Μάλλον λίγο ζόρι να βρούμε πρωταρχική λύση εδώ για να πάρουμε μετά τον αναδρομικό αλγόριθμο.
. Μάλλον λίγο ζόρι να βρούμε πρωταρχική λύση εδώ για να πάρουμε μετά τον αναδρομικό αλγόριθμο. .
.![Z[i\sqrt{2}] Z[i\sqrt{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/44a8940c6a2c607d2ef0d7aa02bc147c.png) είναι UFD, το παραπάνω βέβαια είναι στο
είναι UFD, το παραπάνω βέβαια είναι στο ![Z[\sqrt{2}] Z[\sqrt{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/b42c028445420661476d1cf765e4cae5.png) , και δεν είμαι σίγουρος αν μπορούμε να δουλέψουμε ανάλογα (το 7 μάλιστα δεν είναι πρώτος σε αυτό τον δακτύλιο). Έχω την εντύπωση πως ο τελευταίος δακτύλιος είναι UFD, αν ισχύουν αυτά μπορώ να προχωρήσω σε λύση, αλλιώς μάλλον πρέπει να αλλάξουμε προσέγγιση.
, και δεν είμαι σίγουρος αν μπορούμε να δουλέψουμε ανάλογα (το 7 μάλιστα δεν είναι πρώτος σε αυτό τον δακτύλιο). Έχω την εντύπωση πως ο τελευταίος δακτύλιος είναι UFD, αν ισχύουν αυτά μπορώ να προχωρήσω σε λύση, αλλιώς μάλλον πρέπει να αλλάξουμε προσέγγιση. , όπου
, όπου  , ώστε
, ώστε  .
. ώστε
ώστε  .
. και κάθε πρώτο
και κάθε πρώτο  , ισχύει ότι ο
, ισχύει ότι ο  δεν διαιρεί τον
δεν διαιρεί τον  .
.Έστω, προς άτοπο, ότι
 . Τότε
. Τότε  (αφού
(αφού  ) άρα
) άρα  .
. σε γινόμενο πρώτων παραγόντων, έχουμε ότι
σε γινόμενο πρώτων παραγόντων, έχουμε ότι  .
. , και αφού
, και αφού  , θα είναι
, θα είναι  , άτοπο.
, άτοπο.Έστω
 το σύνολο των περιττών που περιέχονται στο
το σύνολο των περιττών που περιέχονται στο  . Από το θεμελιώδες θεώρημα της αριθμητικής είναι άμεσο ότι κάθε στοιχείο
. Από το θεμελιώδες θεώρημα της αριθμητικής είναι άμεσο ότι κάθε στοιχείο  γράφεται με μοναδικό τρόπο ως
γράφεται με μοναδικό τρόπο ως  όπου
όπου  και
και  . Ορίζουμε
. Ορίζουμε  με
με  .
.  άρα
άρα  . Όμως
. Όμως  άρα η
άρα η  δεν είναι
δεν είναι  , δηλαδή υπάρχουν
, δηλαδή υπάρχουν  έτσι ώστε
έτσι ώστε  . Αν
. Αν  , τότε
, τότε  , ενώ αν
, ενώ αν  , τότε
, τότε  .
.Πολύ όμορφη λύση.giannispapav έγραψε: ↑Πέμ Μάιος 30, 2024 12:06 amΈστωτο σύνολο των περιττών που περιέχονται στο
. Από το θεμελιώδες θεώρημα της αριθμητικής είναι άμεσο ότι κάθε στοιχείο
γράφεται με μοναδικό τρόπο ως
όπου
και
. Ορίζουμε
με
.
Είναιάρα
. Όμως
άρα η
δεν είναι
, δηλαδή υπάρχουν
έτσι ώστε
. Αν
, τότε
, ενώ αν
, τότε
.
 στην εκφώνηση, το οποίο καλύπτεται από την συγκεκριμένη λύση.
στην εκφώνηση, το οποίο καλύπτεται από την συγκεκριμένη λύση. ώστε να υπάρχουν
ώστε να υπάρχουν  διαδοχικοί ακέραιοι με άθροισμα τετραγώνων πρώτο αριθμό.
διαδοχικοί ακέραιοι με άθροισμα τετραγώνων πρώτο αριθμό.Ο
 εύκολα δεν ικανοποιεί την
εύκολα δεν ικανοποιεί την  . Έστω τώρα ότι ο (σε πρωτογενή παραγοντοποίηση)
. Έστω τώρα ότι ο (σε πρωτογενή παραγοντοποίηση)  την ικανοποιεί.
την ικανοποιεί.  και ότι
και ότι  . Πράγματι, υποθέτουμε πρώτα ότι
. Πράγματι, υποθέτουμε πρώτα ότι  , όπου
, όπου  πρώτος.
πρώτος. έχουμε:
έχουμε: 


 διαδοχικοί ακέραιοι αποτελούν πλήρες σύστημα υπολοίπων
διαδοχικοί ακέραιοι αποτελούν πλήρες σύστημα υπολοίπων  .
. και
και  οπότε
οπότε  .
. 
 (εύκολος έλεγχος), η
(εύκολος έλεγχος), η  δεν ικανοποιείται.
δεν ικανοποιείται. , τότε:
, τότε:


 σύνθετος.
σύνθετος. , τότε
, τότε  άρτιος μεγαλύτερος του
άρτιος μεγαλύτερος του  οπότε σύνθετος.
οπότε σύνθετος. που είναι όλες δεκτές:
που είναι όλες δεκτές: πρώτος
πρώτος πρώτος
πρώτος πρώτος
πρώτοςΩραιότατη η προηγούμενη λύση, αλλά ας δούμε μια τελείως στοιχειώδη και απλή:
 , ακριβέστερα
, ακριβέστερα  , έχουμε με το χέρι τις εκδοχές α)
, έχουμε με το χέρι τις εκδοχές α)  διότι
διότι  πρώτος, β)
πρώτος, β)  διότι
διότι  πρώτος και γ)
πρώτος και γ)  διότι
διότι  πρώτος. Οι
πρώτος. Οι  και
και  αποκλείονται διότι
αποκλείονται διότι έχουμε
έχουμε  ίσον άρτιος
ίσον άρτιος  ως άθροισμα δύο άρτιων και δύο περιττών άρα απορρίπτεται και όμοια
ως άθροισμα δύο άρτιων και δύο περιττών άρα απορρίπτεται και όμοια  ίσον σύνθετος, άρα απορρίπτεται.
ίσον σύνθετος, άρα απορρίπτεται.  περαν από τις προηγούμενες.
περαν από τις προηγούμενες.  είναι της μορφής
είναι της μορφής  ή
ή  ή
ή  ή
ή  ή
ή  ή
ή  με
με  (το πρώτο για
(το πρώτο για  ). Τα εξετάζουμε χωριστά αφού πρώτα παρατηρήσουμε ότι το άθροισμα που εξετάζουμε γράφεται
). Τα εξετάζουμε χωριστά αφού πρώτα παρατηρήσουμε ότι το άθροισμα που εξετάζουμε γράφεται ![m^2+(m+1)^2+...+(m+x-1)^2 = \left [ 1^2+2^2 +...+ (m+x-1)^2\right ]- \left [ 1^2+2^2 +...+ (m-1)^2\right ] = m^2+(m+1)^2+...+(m+x-1)^2 = \left [ 1^2+2^2 +...+ (m+x-1)^2\right ]- \left [ 1^2+2^2 +...+ (m-1)^2\right ] =](/forum/ext/geomar/texintegr/latexrender/pictures/84f008c8eaa40520ae9820405db5c2a0.png)

![=\frac {1}{6} x(6A+ x^2-3x+1)= \frac {1}{6} x\left [6A+ (2x-1)(x-1)\right ] \, (*) =\frac {1}{6} x(6A+ x^2-3x+1)= \frac {1}{6} x\left [6A+ (2x-1)(x-1)\right ] \, (*)](/forum/ext/geomar/texintegr/latexrender/pictures/cd49f69cc6b6e6c5ab97ce6071f84c0f.png)
 τότε το δεξί μέλος της
τότε το δεξί μέλος της  ισούται
ισούται  που είναι σύνθετος, οπότε αυτή η περίπτωση απορρίπτεται.
που είναι σύνθετος, οπότε αυτή η περίπτωση απορρίπτεται.  τότε το δεξί μέλος της
τότε το δεξί μέλος της  ισούται
ισούται ![x\left [A+ (2x-1)\frac {x-1}{6}\right ] = x\left [A+ (2x-1) N\right ] x\left [A+ (2x-1)\frac {x-1}{6}\right ] = x\left [A+ (2x-1) N\right ]](/forum/ext/geomar/texintegr/latexrender/pictures/7db1f5e1898e313c952b47aae554ea56.png) που είναι σύνθετος, οπότε αυτή η περίπτωση απορρίπτεται.
που είναι σύνθετος, οπότε αυτή η περίπτωση απορρίπτεται. τότε το δεξί μέλος της
τότε το δεξί μέλος της  ισούται
ισούται ![\frac {6N+2} {2}\left [\frac {6A}{3} + \frac {(12N+3)(x-1)}{3}\right ] = (3N+1)\left [2A+ (4N+1)(x-1)\right ] \frac {6N+2} {2}\left [\frac {6A}{3} + \frac {(12N+3)(x-1)}{3}\right ] = (3N+1)\left [2A+ (4N+1)(x-1)\right ]](/forum/ext/geomar/texintegr/latexrender/pictures/105f8b46cf317c8a9db3b184c5e30591.png) που είναι σύνθετος, οπότε αυτή η περίπτωση απορρίπτεται.
που είναι σύνθετος, οπότε αυτή η περίπτωση απορρίπτεται. τότε το δεξί μέλος της
τότε το δεξί μέλος της  ισούται
ισούται ![\frac {6N+3}{3}\left [\frac {6A}{2}+ (2x-1)\frac {6N+2}{2}\right ] = (2N+1)\left [3A+ (2x-1) (3N+1)\right ] \frac {6N+3}{3}\left [\frac {6A}{2}+ (2x-1)\frac {6N+2}{2}\right ] = (2N+1)\left [3A+ (2x-1) (3N+1)\right ]](/forum/ext/geomar/texintegr/latexrender/pictures/716d5391197c81c64df3ea0e01f40ed6.png) που είναι σύνθετος, οπότε αυτή η περίπτωση απορρίπτεται.
που είναι σύνθετος, οπότε αυτή η περίπτωση απορρίπτεται. τότε το δεξί μέλος της
τότε το δεξί μέλος της  ισούται
ισούται ![\frac {6N+4}{2}\left [\frac {6A}{3}+ (2x-1)\frac {6N+3}{3}\right ] = (3N+2)\left [2A+ (2x-1) (2N+1)\right ] \frac {6N+4}{2}\left [\frac {6A}{3}+ (2x-1)\frac {6N+3}{3}\right ] = (3N+2)\left [2A+ (2x-1) (2N+1)\right ]](/forum/ext/geomar/texintegr/latexrender/pictures/783daf2753fe0845f44a856e89b5f213.png) που είναι σύνθετος, οπότε αυτή η περίπτωση απορρίπτεται.
που είναι σύνθετος, οπότε αυτή η περίπτωση απορρίπτεται. τότε το δεξί μέλος της
τότε το δεξί μέλος της  ισούται
ισούται ![x\left [\frac {6A}{6}+ \frac {12N+9}{3}\frac {6N+4}{2}\right ] = x\left [A+ (4N+3) (3N+2)\right ] x\left [\frac {6A}{6}+ \frac {12N+9}{3}\frac {6N+4}{2}\right ] = x\left [A+ (4N+3) (3N+2)\right ]](/forum/ext/geomar/texintegr/latexrender/pictures/204fac37158254f02bc761f7c84bfe62.png) που είναι σύνθετος, οπότε αυτή η περίπτωση απορρίπτεται.
που είναι σύνθετος, οπότε αυτή η περίπτωση απορρίπτεται. βαθμού
βαθμού  με ακέραιους συντελεστές.
με ακέραιους συντελεστές. , υπάρχουν το πολύ
, υπάρχουν το πολύ  ακέραιοι
ακέραιοι  ώστε
ώστε  , όπου στην παράσταση
, όπου στην παράσταση  , συνθέτουμε την
, συνθέτουμε την  ,
,  φορές.
φορές. για κάποιους ακέραιους
για κάποιους ακέραιους  .
.Ωραία! Μπορεί να βελτιωθεί αυτό;
 ;
; ;
; ) στους ακεραίους το σύστημα
) στους ακεραίους το σύστημα  ,
,  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Bing [Bot] και 1 επισκέπτης