 του μικτόγραμμου τετραπλεύρου
του μικτόγραμμου τετραπλεύρου  , με τέσσερις (!)
, με τέσσερις (!) τουλάχιστον διαφορετικούς τρόπους . Γράψτε αυτόν που σας φαίνεται βολικότερος .
Συντονιστής: emouroukos
 του μικτόγραμμου τετραπλεύρου
του μικτόγραμμου τετραπλεύρου  , με τέσσερις (!)
, με τέσσερις (!) ![\displaystyle{\begin{tikzpicture}[scale=0.7]
\draw[->] (-0.5, 0) -- (2.5, 0) node[below]{x};
\draw[->] (0, -0.5) -- (0, 7.5) node[left]{y};
\draw (0, 0) node[below left]{O};
\draw (1, 0) node[below]{1};
\draw (2, 0) node[below]{2};
\draw[dashed] (0, 2) -- (1, 2) -- (1, 0);
\draw[dashed] (0, 2) -- (2, 2);
\draw[dashed] (0, 7) -- (2, 7) -- (2,0);
\draw (2, 7) node[right]{T};
\draw (0, 7) node[left]{Q};
\draw (0, 2) node[left]{P};
\draw (2, 2) node[right]{S};
%draw area
\fill[lightgray, domain=1:2] plot(\x,{( (\x)^3+ 3*(\x) )/2} ) -- (2, 7) -- (0, 7) -- (0, 2) -- (1, 2);
\draw[line width=1.2pt] plot[smooth,domain=0:2] (\x, {( (\x)^3+ 3*(\x) )/2});
\end{tikzpicture}} \displaystyle{\begin{tikzpicture}[scale=0.7]
\draw[->] (-0.5, 0) -- (2.5, 0) node[below]{x};
\draw[->] (0, -0.5) -- (0, 7.5) node[left]{y};
\draw (0, 0) node[below left]{O};
\draw (1, 0) node[below]{1};
\draw (2, 0) node[below]{2};
\draw[dashed] (0, 2) -- (1, 2) -- (1, 0);
\draw[dashed] (0, 2) -- (2, 2);
\draw[dashed] (0, 7) -- (2, 7) -- (2,0);
\draw (2, 7) node[right]{T};
\draw (0, 7) node[left]{Q};
\draw (0, 2) node[left]{P};
\draw (2, 2) node[right]{S};
%draw area
\fill[lightgray, domain=1:2] plot(\x,{( (\x)^3+ 3*(\x) )/2} ) -- (2, 7) -- (0, 7) -- (0, 2) -- (1, 2);
\draw[line width=1.2pt] plot[smooth,domain=0:2] (\x, {( (\x)^3+ 3*(\x) )/2});
\end{tikzpicture}}](/forum/ext/geomar/texintegr/latexrender/pictures/49301ef7cb9692c28a4934614350231c.png)
 ,
,  ,
,  και
και  . Το
. Το  είναι ορθογώνιο με εμβαδόν
είναι ορθογώνιο με εμβαδόν  τ.μ. Το ζητούμενο εμβαδόν (γραμμοσκιασμένο χωρίο) είναι ίσο με το εμβαδόν του ορθογωνίου μείον το εμβαδόν που περικλείεται της
τ.μ. Το ζητούμενο εμβαδόν (γραμμοσκιασμένο χωρίο) είναι ίσο με το εμβαδόν του ορθογωνίου μείον το εμβαδόν που περικλείεται της 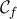 , των ευθειών
, των ευθειών  ,
,  και
και  . Όμως, το τελευταίο εμβαδόν είναι ίσο με
. Όμως, το τελευταίο εμβαδόν είναι ίσο με
 τ.μ.
τ.μ.
Γίνεται και με απ’ ευθείας ένα ολοκλήρωμα :

 είναι γνήσια μονότονη με συνεχή παράγωγο στο
είναι γνήσια μονότονη με συνεχή παράγωγο στο ![\left[ {a,b} \right] \left[ {a,b} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/ac63602e938b0782b35d1af5bdbc40c3.png) τότε:
τότε: .
.Μέλη σε αυτήν τη Δ. Συζήτηση: gbaloglou και 2 επισκέπτες