ΘΑΛΗΣ 2025-2026 (ΘΕΜΑΤΑ ΚΑΙ ΛΥΣΕΙΣ)

#1

Δείτε τα σημερινά θέματα του διαγωνισμού "Ο ΘΑΛΗΣ" στα επισυναπτόμενα αρχεία.

Παρακαλούμε όπως δίνονται πλήρεις λύσεις στα παρακάτω θέματα, όπως απαιτεί ο κανονισμός του forum.

Σχόλιο (8/11/2025- 8:30μμ).
Ενημέρωση link (10/11/2025 - 1:40μμ). Οι επίσημες ενδεικτικές λύσεις της Επιτροπής Διαγωνισμών της ΕΜΕ έχουν αναρτηθεί εδώ.

Φιλικά,

Αχιλλέας

Fotis34 · #2

Στο πρώτο θέμα της Α λυκείου:
Έστω d το τελευταίο ψηφίο του αριθμού Α.
Α=2025•d, το 2025 τελειώνει σε 5 όταν το d:
Έχουμε 10 περιπτώσεις:
1. 2025•0=0, τελευταίο ψηφίο 0
2. 2025•1=2025, τελευταίο ψηφίο 5
3. 2025•2=4050, τελευταίο ψηφίο 0
4. 2025•3=6075, τελευταίο ψηφίο 5
5. 2025•4=8100, τελευταίο ψηφίο 0
6. 2025•5=10125, τελευταίο ψηφίο 5
7. 2025•6=12150, τελευταίο ψηφίο 0
8. 2025•7=14175, τελευταίο ψηφίο 5
9. 2025•8=16200, τελευταίο ψηφίο 0
10. 2025•9=18225, τελευταίο ψηφίο 5
Μόνο για d=0 ή d=5,
d=0, A δεν είναι ακέραιος
d=5, Α=2025•5=10125
Ο μόνος αριθμός Α με την ιδιότητα αυτήν είναι Α=10125

Dimessi · #3

Γ Λυκείου 1. Έστω $\omega$ η διαφορά της αριθμητικής προόδου.
$a_{na_{m}}-a_{n}=\left ( a_{1}+\left ( na_{m}-1 \right )\omega \right )-\left ( a_{1}+\left ( n-1 \right )\omega \right )=n\omega \left ( a_{m}-1 \right ).$
$\left.\begin{matrix} a_{1}+\left ( m-n-1 \right )\omega =49 & \\a_{1}+\left ( m+n-1 \right )\omega =103 & \\ \end{matrix}\right\}\Rightarrow n\omega =27 .$
$\displaystyle a_{m}=a_{1}+\left ( m-1 \right )\omega =\frac{\left ( a_{1}+\left ( m-n-1 \right )\omega \right )+\left ( a_{1}+\left ( m+n-1 \right )\omega \right )}{2}=\frac{a_{m-n}+a_{m+n}}{2}=76.$
$\displaystyle a_{na_{m}}-a_{n}=27\left ( 76-1 \right )=2025.$

Fotis34 · #4

Β' Γυμνασίου
Πρόβλημα 3:
Σε τετράγωνο, η διαγώνιοι διχοτομούνται κάθετα. Άρα ισχύει η ισότητα γωνιών
ΑΟΔ=ΒΟΔ=ΓΟΔ=ΔΟΑ=90⁰. Επίσης επειδή Ο το σημείο τομείς των ευθειών είναι ΑΟ=ΟΒ=ΟΓ=ΟΔ.
Επειδή από την υπόθεση ΒΔ και ΑΕ είναι παράλληλες, με τέμνουσα την ευθεία ΑΟ , οι γωνίες ΔΟΓ+ΟΑΕ = 180⁰, αφού είναι εντός και επι ταύτα γωνίες, άρα παραπληρωματικές. Όμως ξέρουμε ότι ΔΟΓ=90⁰, άρα είναι ΟΑΕ=180⁰-90⁰=90⁰. Τώρα πάλι από την υπόθεση ότι ΑΓ και ΔΕ είναι παράλληλες και με τέμνουσα την ευθεία ΔΟ ισχύει ότι ΑΟΔ+ΟΔΕ=180⁰, ως εντός και επι ταύτα γωνίες, άρα παραπληρωματικές. Όμως ξέρουμε ότι ΑΟΔ=90⁰, άρα ΟΔΕ=180⁰-90⁰=90⁰. Επειδή το ΑΟΔΕ είναι τετράπλευρο έπεται ότι το άθροισμα των γωνιών του είναι 360. Αφού ξέρουμε της υπόλοιπες τρεις γωνίες
Μπορούμε να βρούμε και την ΑΕΔ. ΑΕΔ=360⁰-(ΑΟΔ+ΟΔΕ+ΕΑΟ) = 360⁰-270⁰=90⁰, άρα το τετράπλευρο ΑΟΔΕ είναι ορθογώνιο παραλληλόγραμμα όμως επειδή έχουμε αποδείξει ΑΟ=ΟΒ έπεται ότι ΑΟ=ΟΔ, αφού το τετράπλευρο ΑΟΔΕ έχει όλες τις γωνίες του ίσες με 90⁰ και έχει δύο διαδοχικές πλευρές ίσες, έπεται ότι είναι τετράγωνο.

Fotis34 · #5

Πολύ ωραία όλα τα θέματα, ευχαριστούμε την επιτροπή διαγωνισμών.

Fotis34 · #6

Β' Γυμνασίου
Πρόβλημα 2 ( νομίζω το πιο όμορφο του διαγωνισμού στα θέματα της Β )
Θέτω για ευκολία α = a, β = b.
Για να είναι ΜΚΔ(a,b)=15, πρέπει οι αριθμοί a,b να είναι πολλαπλάσια του 15. Δηλαδή a= 15x, b= 15y. Στο ΕΚΠ(a,b)=60, αντικαθιστώ και έχω : ΕΚΠ(a,b) = 15 • ΕΚΠ(x,y), ( από την υπόθεση ΕΚΠ(a,b)=60)
60 = 15 • ΕΚΠ(x,y) το οποίο ισοδύναμα αν διαιρέσω και της δύο μεριές με 15 έχω
ΕΚΠ(x,y)=4, από αυτό έπεται ότι x,y διαιρέτες του 4. Άρα έχουμε τρεις περιπτώσεις
Περίπτωση 1: x=1, y=4, η οποία δίνει a=15, y=60, στο οποίο ΕΚΠ(15,60)=60 και ΜΚΔ(15,60)=15, άρα έχουμε το ζεύγος
(a,b)=(15,60).
Περίπτωση 2: x=4, y=1, άτοπο αφού από την υπόθεση a≤b δηλαδή και x≤y.
Περίπτωση 3: x=2, y=2, άρα a=30, b=30 , το οποίο όμως δίνει ΕΚΠ(30,30)=30 , και ΜΚΔ(30,30)=30.
Άρα υπάρχει μόνο ένα ζεύγος με την ιδιότητα αυτήν, το (x,y)=(15,60).

αρψ2400 · #7

Α΄ ΛΥΚΕΙΟΥ
Πρόβλημα 1 (6 μονάδες) Να βρείτε όλους τους θετικούς ακεραίους Α οι οποίοι είναι 2025 φορές μεγαλύτεροι
από το τελευταίο ψηφίο τους.

Έστω $\overline{xy}$ ο αριθμός με

οποιοσδήποτε θετικός και

το τελευταίο ψηφίο . 10x+y=2025y , 10x=2024y , 5x=1012y , y=5 , x=1012

, και ο μοναδικός αριθμός είναι ο 10125

.

Dimessi · #8

Γ Λυκείου 2.
$\left ( 5x^{2}-y^{2}-xy \right )\left ( 5x^{2}-y^{2}+xy \right )=7.$
Αν (x,y)

λύση της

τότε και

λύση της

Υποθέτουμε ότι $y \leqslant x,$ τότε $5x^2-y^2+xy \geqslant 4x^2+xy>0$ και επειδή 5x^2-y^2-xy<5x^2-y^2+xy,

άρα

και

Τότε

οπότε

Υποθέτουμε τώρα ότι x<y.

Αν

έχουμε

άτοπο , αν 5x^2-xy-y^2-xy=-7,5x^2-y^2+xy=-1

έχουμε

οπότε

κι αν

έχουμε

οπότε

Άρα έχουμε λύσεις $\left ( x,y \right )\in \left\{ \left ( 1,3 \right ),\left ( 3,1 \right )\right\}.$

Fotis34 · #9

Γ' Γυμνασίου
Πρόβλημα 2:
100a+10b+c = (10b+c)+8(10a+b)=
100a+10b+c = 10b+c+80a+8b=
(100a-80a)+(10b-18b)=0
20a-8b=0
20a=8b
5a=2b
b= (5/2)a
Επειδή 0≤a,b≤9, πρέπει ο a να είναι άρτιος.
a=2,4,6,8 , b= 5, 10,15,20
Όμως b≤9, άρα έχουμε ότι b=5 και a=2.
Αφού είναι A = 100•2 + 10•5 + c = 250 + c . Για να διαιρείται με το 3 πρέπει να έχει άθροισμα ψηφίων που να διαιρείται με 3.
2+5+c = 7+c, άρα πρέπει 7+c \equiv 0 ( mod 3), το οποίο δίνει c \equiv 2 ( mod 3) , άρα είναι c= 2,5,8 . Άρα οι τριψήφιοι θετικοί ακέραιοι Α με την ιδιότητα αυτήν είναι :
Α = 252 , Α = 255, Α=258.

∫ot.T. · #10

3ο Α' Λυκείου

Έστω

το μέσο του

και

το σημείο τομής της ευθείας $M\Delta$ .
Επίσης $A\Delta = \Delta B$ ως σημείο της μεσοκαθέτου. Από θεώρημα Μενέλαου έχουμε

$\dfrac{\Delta B}{\Delta \Gamma}\cdot \dfrac{E\Gamma}{EA}\cdot \dfrac{MA}{MB}=1$

Άρα $\dfrac{\Delta B}{\Delta \Gamma}=\dfrac{EA}{E\Gamma}$

Όμως το ΕΑΒ

είναι ισοσκελές αφού το

είναι στην μεσοκάθετο και από την δεδομένη γωνία προκύπτει ότι είναι ισόπλευρο.
Άρα EA=AB

Επίσης $E\Gamma = EA + A\Gamma = AB+2AB=3AB$

Άρα $\dfrac{\Delta A}{\Delta \Gamma}=\dfrac{\Delta B}{\Delta \Gamma}=\dfrac{EA}{E\Gamma}=\dfrac{1}{3}$

∫ot.T. · #11

Dimessi έγραψε: ↑
Παρ Νοέμ 07, 2025 4:44 pm
Γ Λυκείου 2.
$\left ( 5x^{2}-y^{2}-xy \right )\left ( 5x^{2}-y^{2}+xy \right )=7.$
Αν λύση της τότε και λύση της Υποθέτουμε ότι $y \leqslant x,$ τότε $5x^2-y^2+xy \geqslant 4x^2+xy>0$ και επειδή άρα και Τότε οπότε Υποθέτουμε τώρα ότι Αν έχουμε άτοπο , αν έχουμε οπότε κι αν έχουμε οπότε
Άρα έχουμε λύσεις $\left ( x,y \right )\in \left\{ \left ( 1,3 \right ),\left ( 3,1 \right )\right\}.$

Το

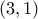δεν επαληθεύει την εξίσωση. Η μοναδική λύση είναι (1,3)

Dinhoo37 · #12

Μου κάνει εντύπωση το πόσο εύκολο ήταν το πρώτο θέμα της Α Λυκείου συγκριτικά με τα άλλα. Μόνο εγώ είμαι?

∫ot.T. · #13

Dinhoo37 έγραψε: ↑
Παρ Νοέμ 07, 2025 5:09 pm
Μου κάνει εντύπωση το πόσο εύκολο ήταν το πρώτο θέμα της Α Λυκείου συγκριτικά με τα άλλα. Μόνο εγώ είμαι?

Το πρώτο θέμα θα είναι (σχεδόν) πάντα πιο εύκολο από όλα τα άλλα. Αλλά ίσως (συγκριτικά με άλλες χρονιές) να ήταν φέτος πιο εύκολο. Το τρίτο θέμα της Α' Λυκείου μου άρεσε, περισσότερο από το δικό μας τρίτο (Γ' Λυκείου).

Dinhoo37 · #14

∫ot.T. έγραψε: ↑
Παρ Νοέμ 07, 2025 5:21 pm

Dinhoo37 έγραψε: ↑
Παρ Νοέμ 07, 2025 5:09 pm
Μου κάνει εντύπωση το πόσο εύκολο ήταν το πρώτο θέμα της Α Λυκείου συγκριτικά με τα άλλα. Μόνο εγώ είμαι?
Το πρώτο θέμα θα είναι (σχεδόν) πάντα πιο εύκολο από όλα τα άλλα. Αλλά ίσως (συγκριτικά με άλλες χρονιές) να ήταν φέτος πιο εύκολο. Το τρίτο θέμα της Α' Λυκείου μου άρεσε, περισσότερο από το δικό μας τρίτο (Γ' Λυκείου).

Το 1ο το έλυσα αρκετά γρήγορα, ωστόσο το 3ο έχω μόνο περίπου το μισό σωστό και για το 2ο περιμένω να δω λύσεις. Ήταν μία αρκετά περίεργη εμπειρία, και ασχέτως αν πέρασα ή όχι είχε πλάκα. Απλά μου έκανε εντύπωση γιατί σχεδόν όποιος έγραψε σήμερα για Α’ Λυκείου το 1ο Θέμα το έχει λυμένο, ή τουλάχιστον όσους ρώτησα.

Dimessi · #15

Γ Λυκείου 3.
Από το εγγράψιμο $BEZ\Gamma \left ( \angle BEZ=\angle B\Gamma Z=90^\circ \right )$ έχουμε $\displaystyle \angle EBZ=\angle E\Gamma Z\overset{\angle BEZ=\angle E\Delta \Gamma =90^\circ}\Rightarrow \vartriangle EBZ\sim \vartriangle E\Delta \Gamma \Rightarrow \frac{\left ( EBZ \right )}{\left ( E\Delta \Gamma \right )}=\left ( \frac{EZ}{E\Delta } \right )^{2}\overset{EZ\parallel A\Gamma }=\left ( \frac{A\Gamma }{A\Delta } \right )^{2}$ $\displaystyle =\frac{\alpha ^{2}+\beta ^{2}}{\beta ^{2}}\left ( 1 \right ).$ Αλλά $\displaystyle \frac{\left ( E\Delta \Gamma \right )}{\left ( AB\Gamma \Delta \right )}=\frac{\left ( E\Delta \Gamma \right )}{2\left ( A\Delta \Gamma \right )}=\frac{E\Delta }{2A\Delta }=\frac{A\Delta -AE}{2A\Delta }\overset{\vartriangle EAB \sim \vartriangle B\Gamma A\Rightarrow AE=\frac{\alpha ^{2}}{\beta }}=\frac{\beta -\frac{\alpha ^{2}}{\beta }}{2\beta }=\frac{\beta ^{2}-\alpha ^{2}}{2\beta ^{2}}\overset{(1)}\Rightarrow$ $\displaystyle \boxed{\frac{\left ( EBZ \right )}{\left ( AB\Gamma \Delta \right )}=\frac{\lambda ^{4}-1}{2\lambda ^{4}}}$

Fotis34 · #16

Πώς σας φάνηκαν τα θέματα όσοι γράψατε για Β γυμνασίου;

Ιστοσελίδα · #17

Έστω ότι ο αριθμός Α έχει n πλήθος ψηφίων, τότε:
$A = \overline{x_n x_{n-1} \ldots x_2 x_1} = 2025\cdot x_1 = 2\cdot 10^3 x_1 + 25\cdot x_1 < 18 \cdot 10^3 + 25 x_1 = 10^4 + 8\cdot 10^3 + 25 x_1$

Οπότε ο Α έχει το πολύ 5 ψηφία και θα γράφεται: $A = \overline{x_5 x_4 x_3 x_2 x_1} = 2025 x_1 \Leftrightarrow$

$x_5 10^4 + x_4 10^3 +x_3 10^2 + x_2 10 + x_1 = 2025 x_1 \Leftrightarrow$

Οπότε x_1 = 0

ή

.

Αν

τότε Α=0 που δεν είναι θετικός

Αν x_1 = 5

τότε $A = \overline{x_5 x_4 x_3 x_2 5} = 2025 \cdot 5 = 11.125$

mick7 · #18

Α Λυκείου Πρόβλημα 2

Η παράσταση γράφεται (2x+3y−1)^2+(xy+3)^2=0

και η ζητούμενη τιμή είναι

Nikitas K. · #19

Α' Λυκείου Πρόβλημα 3

x := AB

Εφαρμόζοντας διαδοχικά

φορές το νόμο συνημιτόνων στο $\triangle ABC$ λαμβάνουμε:

$a^2 \overset{\angle A = 120^\circ}{=} x^2 + (2x)^2 - 2x (2x) \cos 120^\circ \Leftrightarrow a = \sqrt{7} x ~\color{blue} *$

και

$(2x)^2 \overset{{\color{blue} *}}{=} x^2 + (\sqrt{7} x)^2 - 2x (\sqrt{7}x)\cos{\angle B}\Leftrightarrow \cos \angle B = \dfrac{2}{\sqrt{7}}\Leftrightarrow \dfrac{\dfrac{x}{2}}{B\Delta} = \dfrac{2}{\sqrt{7}} \overset{A\Delta = B\Delta}\Leftrightarrow A\Delta = \dfrac{x\sqrt{7}}{4} ~\color{blue} **$

Ισχύει ότι:
$\Delta\Gamma \underset{ {\color{blue} **} }{ \overset{{\color{blue} *} }{ = } } \sqrt{7} x - \dfrac{x\sqrt{7}}{4} = \dfrac{3x\sqrt{7}}{4} \Leftrightarrow \dfrac{A\Delta}{\Delta\Gamma} \overset{{\color{blue} **}} {=} \dfrac{1}{3}$

Fotis34 · #20

Θα μπορούσε κάποιος να μου απαντήσει για το πρόβλημα 2 της Β γυμνασίου. Ευχαριστώ εκ των προτέρων.

ΘΑΛΗΣ 2025-2026 (ΘΕΜΑΤΑ ΚΑΙ ΛΥΣΕΙΣ)

ΘΑΛΗΣ 2025-2026 (ΘΕΜΑΤΑ ΚΑΙ ΛΥΣΕΙΣ)

Re: ΘΑΛΗΣ 2025-2026 (ΘΕΜΑΤΑ ΚΑΙ ΛΥΣΕΙΣ)

Re: ΘΑΛΗΣ 2025-2026 (ΘΕΜΑΤΑ ΚΑΙ ΛΥΣΕΙΣ)

Re: ΘΑΛΗΣ 2025-2026 (ΘΕΜΑΤΑ ΚΑΙ ΛΥΣΕΙΣ)

Re: ΘΑΛΗΣ 2025-2026 (ΘΕΜΑΤΑ ΚΑΙ ΛΥΣΕΙΣ)

Re: ΘΑΛΗΣ 2025-2026 (ΘΕΜΑΤΑ ΚΑΙ ΛΥΣΕΙΣ)

Re: ΘΑΛΗΣ 2025-2026 (ΘΕΜΑΤΑ ΚΑΙ ΛΥΣΕΙΣ)

Re: ΘΑΛΗΣ 2025-2026 (ΘΕΜΑΤΑ ΚΑΙ ΛΥΣΕΙΣ)

Re: ΘΑΛΗΣ 2025-2026 (ΘΕΜΑΤΑ ΚΑΙ ΛΥΣΕΙΣ)

Re: ΘΑΛΗΣ 2025-2026 (ΘΕΜΑΤΑ ΚΑΙ ΛΥΣΕΙΣ)

Re: ΘΑΛΗΣ 2025-2026 (ΘΕΜΑΤΑ ΚΑΙ ΛΥΣΕΙΣ)

Re: ΘΑΛΗΣ 2025-2026 (ΘΕΜΑΤΑ ΚΑΙ ΛΥΣΕΙΣ)

Re: ΘΑΛΗΣ 2025-2026 (ΘΕΜΑΤΑ ΚΑΙ ΛΥΣΕΙΣ)

Re: ΘΑΛΗΣ 2025-2026 (ΘΕΜΑΤΑ ΚΑΙ ΛΥΣΕΙΣ)

Re: ΘΑΛΗΣ 2025-2026 (ΘΕΜΑΤΑ ΚΑΙ ΛΥΣΕΙΣ)

Re: ΘΑΛΗΣ 2025-2026 (ΘΕΜΑΤΑ ΚΑΙ ΛΥΣΕΙΣ)

Re: ΘΑΛΗΣ 2025-2026 (ΘΕΜΑΤΑ ΚΑΙ ΛΥΣΕΙΣ)

Re: ΘΑΛΗΣ 2025-2026 (ΘΕΜΑΤΑ ΚΑΙ ΛΥΣΕΙΣ)

Re: ΘΑΛΗΣ 2025-2026 (ΘΕΜΑΤΑ ΚΑΙ ΛΥΣΕΙΣ)

Re: ΘΑΛΗΣ 2025-2026 (ΘΕΜΑΤΑ ΚΑΙ ΛΥΣΕΙΣ)

Μέλη σε σύνδεση