Θέματα της πρώτης μέρας για την 10η τάξη.
1. Έστω
και 
διαφορετικοί πρώτοι αριθμοί. Δίνεται μια άπειρη φθίνουσα αριθμητική πρόοδος, στην οποία συναντάται ο καθένας εκ των αριθμών 
και 
. Να αποδείξετε ότι σε αυτήν την πρόοδο απαραίτητα θα εμφανιστούν και οι αριθμοί και . (Α. Κουζνέτσοβ, Επιτροπή διαγωνισμού)2. Δίνεται ένας περιττός αριθμός
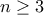. Σε ένα τετραγωνισμένο τετράγωνο 
χρωματίστηκαν 
κελιά. Ποιος είναι ο μεγαλύτερος αριθμός γωνιών των τριών κελιών που μπορούν εγγυημένα να αποκοπούν από το μη χρωματισμένο τετραγωνισμένο σχήμα; (Γκ. Σαραφετντίνοβα)3. Δίνεται ένας μη μηδενικός αριθμός
. Ο Γιώργος σκέφτηκε ένα ζεύγος διαφορετικών πολυωνύμων βαθμού (με πραγματικούς συντελεστές), ομοίως ο Άρης σκέφτηκε ένα ζεύγος διαφορετικών πολυωνύμων βαθμού . Η Ελένη ξέρει το : σκοπός της είναι να αποφανθεί, αν είναι άραγε ίσα τα ζεύγη πολυώνυμων του Γιώργου και Άρη. Η Ελένη επιλέγει μια συλλογή 
πραγματικών αριθμών 
και ανακοινώνει αυτούς τους αριθμούς. Ως απάντηση ο Γιώργος συμπληρώνει έναν πίνακα 
: για κάθε 
γράφει στα δυο κελιά της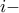 
οστής στήλης το ζεύγος των αριθμών 
(σε οποιαδήποτε από τις δυο δυνατές διατάξεις), όπου 
και 
, τα δυο πολυώνυμα που σκέφτηκε. Ανάλογο πίνακα συμπληρώνει και ο Άρης. Για ποιο ελάχιστο θα μπορέσει η Ελένη (εξετάζοντας τους πίνακες) με σιγουριά να επιτύχει τον σκοπό της; (Λ. Σατούνοβ)4. Δίνεται ένα κυρτό τετράπλευρο
, στο οποίο 
και οι διαγώνιοί του τέμνονται στο σημείο 
. Η ευθεία 
τέμνει τα τμήματα 
και 
στα σημεία 
και 
αντίστοιχα. Είναι γνωστό ότι 
και 
. Να αποδείξετε, ότι το μήκος του τμήματος 
δεν είναι μεγαλύτερο της διαμέτρου του περιγεγραμμένου κύκλου του τριγώνου 
. (Α. Κουζνέτσοβ)