Θέματα της 2ης μέρας για την 11η τάξη. 1 Φεβρουαρίου 2024.
1. Ένας δάσκαλος έχει
σταθμά μάζας 
γχρ , 
χγρ, …, χγρ. Θέλει να δώσει από 
σταθμά στον Γιώργο και στον Νίκο έτσι, ώστε να ικανοποιείται η ακόλουθη συνθήκη: καμία εντεκάδα σταθμών του Γιώργου να μην είναι ισόβαρη με καμία δωδεκάδα σταθμών του Νίκου και ομοίως καμία ενδεκάδα σταθμών του Νίκου να μην είναι ισόβαρη με καμία δωδεκάδα σταθμών του Γιώργου. Μπορεί άραγε ο δάσκαλος να το επιτύχει; (Ο. Ποντλίνσκϊι)2. Η γραφική παράσταση
ενός δευτεροβάθμιου πολυώνυμου 
με πραγματικούς συντελεστές τέμνει την γραφική παράσταση 
του δευτεροβάθμιου πολυώνυμου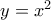 
στα σημεία 
και 
. Οι εφαπτόμενες στα σημεία και της γραφικής παράστασης τέμνονται στο σημείο 
. Προέκυψε, ότι το σημείο βρίσκεται στην γραφική παράσταση . Να βρείτε όλες τις δυνατές τιμές του 
. (Α. Τερέσιν)3. Στο χώρο δίνονται τρία ευθύγραμμα τμήματα
, 
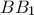και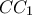 
με κοινό μέσο το σημείο 
. Προέκυψε, ότι η σφαίρα 
, περιγεγραμμένη γύρω από το τετράεδρο 
, εφάπτεται του επιπέδου 
στο σημείο 
. Το σημείο 
είναι το κέντρο του περιγεγραμμένου κύκλου του τριγώνου . Να αποδείξετε, ότι 
. (Α. Κουζνέτσοβ)4. Ένα ισόπλευρο τρίγωνο
πλευράς μήκους 
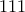διαμερίστηκε με ευθείες, παράλληλες προς τις πλευρές του, σε ισόπλευρα τρίγωνα πλευράς . Όλες οι κορυφές αυτών των τριγώνων, εκτός του κέντρου του τριγώνου , είναι σημειωμένα. Θα ονομάσουμε ένα σύνολο μερικών εκ των σημειωμένων σημείων γραμμικό, αν όλα αυτά τα σημεία βρίσκονται στην ίδια ευθεία, παράλληλη προς πλευρά του . Πόσοι τρόποι υπάρχουν να διαμερίσουμε όλα τα σημειωμένα σημεία σε 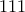γραμμικά σύνολα; (Οι τρόποι, που διαφέρουν στην διάταξη των συνόλων, θεωρούνται ίδιοι) (Ι. Μπογκντάνοβ) 5. Δίνεται ένας φυσικός αριθμός
. Αρχικά στον πίνακα είναι γραμμένος ο αριθμός . Κάθε λεπτό η Άννα αναπαριστά αριθμό γραμμένο στον πίνακα, ως άθροισμα δυο άνισων θετικών ανάγωγων κλασμάτων και η Άρτεμις αφήνει στον πίνακα μόνο ένα από αυτά τα δυο κλάσματα. Να αποδείξετε, ότι η Άννα μπορεί να καταφέρει, ώστε ο παρονομαστής του κλάσματος, που θα μείνει σε 
λεπτά να μην υπερβαίνει τον 
ανεξάρτητα το τι θα πράξει η Άρτεμις. (Μ. Ντίντιν)
έχει προφανώς δύο διαφορετικές μεταξύ τους λύσεις, συνεπώς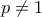 
και:
και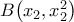 
, όπου 
, 
οι λύσεις της 
. Για τις συντεταγμένες του 
ισχύει:![\displaystyle{
\left\{\begin{array}{ll}
y_0 - x_1^2 = 2 x_1 \bigl( x_0 - x_1 \bigr) \\[0.05in]
y_0 - x_2^2 = 2 x_2 \bigl( x_0 - x_2 \bigr)
\end{array}\right.
\Leftrightarrow
\left\{\begin{array}{ll}
y_0 = 2 x_1 \cdot x_0 - x_1 ^2 \\[0.05in]
y_0 = 2 x_2 \cdot x_0 - x_2 ^2
\end{array}\right.
\Leftrightarrow \ldots \Leftrightarrow
\left\{\begin{array}{ll}
x_0 = \dfrac{x_1 + x_2}{2} \\[0.1in]
y_0 = x_1 x_2
\end{array}\right.
\overset{\; \rm Vieta \ }{\Leftarrow\joinrel=\joinrel=\joinrel \Rightarrow}
\left\{\begin{array}{ll}
x_0 = \dfrac{-q}{2(p - 1)} \\[0.2in]
y_0 = \dfrac{r}{p - 1}
\end{array}\right.
}](/forum/ext/geomar/texintegr/latexrender/pictures/21e4abdd43551108787b6c00416bfe15.png "\displaystyle{
\left\{\begin{array}{ll}
y_0 - x_1^2 = 2 x_1 \bigl( x_0 - x_1 \bigr) \\[0.05in]
y_0 - x_2^2 = 2 x_2 \bigl( x_0 - x_2 \bigr)
\end{array}\right.
\Leftrightarrow
\left\{\begin{array}{ll}
y_0 = 2 x_1 \cdot x_0 - x_1 ^2 \\[0.05in]
y_0 = 2 x_2 \cdot x_0 - x_2 ^2
\end{array}\right.
\Leftrightarrow \ldots \Leftrightarrow
\left\{\begin{array}{ll}
x_0 = \dfrac{x_1 + x_2}{2} \\[0.1in]
y_0 = x_1 x_2
\end{array}\right.
\overset{\; \rm Vieta \ }{\Leftarrow\joinrel=\joinrel=\joinrel \Rightarrow}
\left\{\begin{array}{ll}
x_0 = \dfrac{-q}{2(p - 1)} \\[0.2in]
y_0 = \dfrac{r}{p - 1}
\end{array}\right.
}")
![\displaystyle{
C \in G_1
\Leftrightarrow p \biggl[ \dfrac{-q}{2(p - 1)} \biggr]^2 - \dfrac{q^2}{2(p - 1)} + r = \dfrac{r}{p - 1}
\Leftrightarrow \ldots \overset{\ p \; \ne \; 1}{\Leftarrow\joinrel=\joinrel=\joinrel\Rightarrow}
(p - 2) \Bigl[ q^2 - 4(p - 1)r \Bigr] = 0
\overset{(2)}{\Leftarrow\joinrel=\joinrel\Rightarrow} \boxed{p = 2}
}](/forum/ext/geomar/texintegr/latexrender/pictures/1c8f6f326dd81f0fc3a5f23e7a6c9fe9.png "\displaystyle{
C \in G_1
\Leftrightarrow p \biggl[ \dfrac{-q}{2(p - 1)} \biggr]^2 - \dfrac{q^2}{2(p - 1)} + r = \dfrac{r}{p - 1}
\Leftrightarrow \ldots \overset{\ p \; \ne \; 1}{\Leftarrow\joinrel=\joinrel=\joinrel\Rightarrow}
(p - 2) \Bigl[ q^2 - 4(p - 1)r \Bigr] = 0
\overset{(2)}{\Leftarrow\joinrel=\joinrel\Rightarrow} \boxed{p = 2}
}")