Οι θετικοί πραγματικοί αριθμοί
 και
και  είναι τέτοιοι, ώστε
είναι τέτοιοι, ώστε 
Να αποδείξετε ότι

ΘΕΜΑ 2
Να προσδιορίσετε όλους τους θετικούς ακέραιους
 για τους οποίους υπάρχουν θετικοί ακέραιοι
για τους οποίους υπάρχουν θετικοί ακέραιοι  τέτοιοι, ώστε
τέτοιοι, ώστε και
και  το σύνολο
το σύνολο  είναι το σύνολο των θετικών διαιρετών του αριθμού
είναι το σύνολο των θετικών διαιρετών του αριθμού 
ΘΕΜΑ 3
Θεωρούμε παραλληλόγραμμο
 το σημείο τομής των διαγωνίων του,
το σημείο τομής των διαγωνίων του, και το μέσο
και το μέσο  της πλευράς
της πλευράς 
Έστω
 σημείο του τμήματος
σημείο του τμήματος  και
και  το σημείο τομής των ευθειών
το σημείο τομής των ευθειών 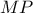 και
και  Η παράλληλη στην
Η παράλληλη στην 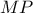 από το
από το  τέμνει την ευθεία
τέμνει την ευθεία  στο σημείο
στο σημείο 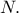 Να αποδείξετε ότι τα σημεία
Να αποδείξετε ότι τα σημεία  και
και  είναι συνευθειακά αν και μόνο αν το
είναι συνευθειακά αν και μόνο αν το  είναι το μέσο του
είναι το μέσο του 
ΘΕΜΑ 4
Να προσδιορίσετε το μικρότερο θετικό ακέραιο
 για τον οποίο ισχύει:
για τον οποίο ισχύει: Για οποιονδήποτε χρωματισμό των αριθμών του συνόλου
 με δύο χρώματα, υπάρχουν
με δύο χρώματα, υπάρχουν  με το ίδιο χρώμα τέτοιοι, ώστε
με το ίδιο χρώμα τέτοιοι, ώστε 

 θα είναι
θα είναι 
 θα είναι
θα είναι  παραλ/μμο άρα
παραλ/μμο άρα 
 παραλ/μμο, άρα
παραλ/μμο, άρα  .Επομένως
.Επομένως  κι από
κι από  συγκλίνουν στο
συγκλίνουν στο 
 συντρέχουν ,
συντρέχουν , και
και  θα είναι (θ.κ.δ) και
θα είναι (θ.κ.δ) και 
 το
το 



 , δηλαδή ότι:
, δηλαδή ότι: , (1)
, (1) . Τότε
. Τότε  και άρα:
και άρα: 
 , ή αρκεί:
, ή αρκεί: , ή
, ή , ή
, ή  , το οποίο είναι αληθές.
, το οποίο είναι αληθές.
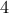 είναι το
είναι το 
 . Άρα
. Άρα 
 . Άρα
. Άρα 
 . Άρα
. Άρα 
 που είναι
που είναι  , εύκολα διαπιστώνουμε ότι δεν μπορούν να εμφανισθούν.
, εύκολα διαπιστώνουμε ότι δεν μπορούν να εμφανισθούν.![a+b+c \geq 3\sqrt[3]{abc} => 3\sqrt[3]{abc} \leq 3 => abc \leq 1 a+b+c \geq 3\sqrt[3]{abc} => 3\sqrt[3]{abc} \leq 3 => abc \leq 1](/forum/ext/geomar/texintegr/latexrender/pictures/12ec5435d36920a23f10cfbf463b6818.png)
![a^2 + b^2 + c^2 + a^2b + b^2c + c^2a\geq 6\sqrt[6]{a^5b^5c^5}. a^2 + b^2 + c^2 + a^2b + b^2c + c^2a\geq 6\sqrt[6]{a^5b^5c^5}.](/forum/ext/geomar/texintegr/latexrender/pictures/f3beb9e002ef721644a47a989c456b3f.png)
 (δηλ. 1), έχουμε:
(δηλ. 1), έχουμε:![a^2 + b^2 + c^2 + a^2b + b^2c + c^2a\geq 6\sqrt[6]{1} => a^2 + b^2 + c^2 + a^2b + b^2c + c^2a\geq 6. a^2 + b^2 + c^2 + a^2b + b^2c + c^2a\geq 6\sqrt[6]{1} => a^2 + b^2 + c^2 + a^2b + b^2c + c^2a\geq 6.](/forum/ext/geomar/texintegr/latexrender/pictures/cdcec88aa3ccc9c2e459ecead02bc77c.png)
![a^2 + b^2 + c^2 + a^2b + b^2c + c^2a\geq 6\sqrt[6]{1} a^2 + b^2 + c^2 + a^2b + b^2c + c^2a\geq 6\sqrt[6]{1}](/forum/ext/geomar/texintegr/latexrender/pictures/730e690a34427c2d669b6d05c37d85d3.png)
 με
με  μεταβλητά, δεν έπεται ότι
μεταβλητά, δεν έπεται ότι  .
. για
για 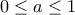 .
.  (άμεσο, αφού
(άμεσο, αφού  ). Τώρα το
). Τώρα το  έχει μέγιστο
έχει μέγιστο  καθώς
καθώς  (άμεσο, αφού
(άμεσο, αφού 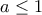 ) με ισότητα όταν
) με ισότητα όταν  .
. . Για παράδειγμα πάρε
. Για παράδειγμα πάρε  για να δεις ότι δεν ισχύει καθώς
για να δεις ότι δεν ισχύει καθώς  .
. , οπότε
, οπότε 
 .
.

 , έπεται
, έπεται 
 είναι
είναι  . Δεν ισχύει. Τα
. Δεν ισχύει. Τα  ικανοποιούν
ικανοποιούν  . Οπότε το καθένα χωριστά μπορεί να πάρει οποιαδήποτε τιμή στο ανοικτό διάστημα
. Οπότε το καθένα χωριστά μπορεί να πάρει οποιαδήποτε τιμή στο ανοικτό διάστημα  . Μάλιστα μπορεί να πλησιάσει το
. Μάλιστα μπορεί να πλησιάσει το  όσο κοντά θέλεις.
όσο κοντά θέλεις.