Σε συνέχεια των προηγούμενων θεμάτων με το 1ο τεστ και το 2ο τεστ, ακολουθούν τα προβλήματα του 3ου τεστ.
Θα χαρούμε να δούμε κι άλλες διαφορετικές λύσεις στα παρακάτω θέματα.
**********************************************
JBMO Practice TEST 3
ΔΙΑΡΚΕΙΑ: 4,5 ΩΡΕΣ
ΘΕΜΑ 1. Τα ύψη
 ,
,  ,
,  ενός οξυγώνιου τριγώνου τέμνονται στο
ενός οξυγώνιου τριγώνου τέμνονται στο  . Έστω
. Έστω  το συμμετρικό του σημείου
το συμμετρικό του σημείου  ως προς την πλευρά
ως προς την πλευρά  , και έστω
, και έστω  το περίκεντρο του τριγώνου
το περίκεντρο του τριγώνου  .
. (α) Να δειχθεί ότι τα σημεία
 είναι ομοκυκλικά.
είναι ομοκυκλικά.(β) Να δειχθεί ότι τα σημεία
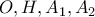 είναι ομοκυκλικά.
είναι ομοκυκλικά.ΘΕΜΑ 2. Δέκα αριθμοί επιλέγονται από τους
 Να δειχθεί ότι μπορούμε να επιλέξουμε τέσσερις διακεκριμμένους αριθμούς από αυτούς τους δέκα, έτσι ώστε το άθροισμα δύο εξ αυτών να ισούται με το άθροισμα των άλλων δύο.
Να δειχθεί ότι μπορούμε να επιλέξουμε τέσσερις διακεκριμμένους αριθμούς από αυτούς τους δέκα, έτσι ώστε το άθροισμα δύο εξ αυτών να ισούται με το άθροισμα των άλλων δύο.ΘΕΜΑ 3. Να δειχθεί ότι αν οι
 είναι θετικοί αριθμοί τέτοιοι ώστε
είναι θετικοί αριθμοί τέτοιοι ώστε  , τότε
, τότε
ΘΕΜΑ 4. Να βρείτε όλους τους θετικούς ακέραιους
 τέτοιους ώστε καθένας από αυτούς να διαιρεί το άθροισμα των υπόλοιπων τριών.
τέτοιους ώστε καθένας από αυτούς να διαιρεί το άθροισμα των υπόλοιπων τριών.**********************************************
Φιλικά,
Αχιλλέας

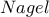 είναι
είναι  και είναι
και είναι 
 συνευθειακά .
συνευθειακά . άρα
άρα 
 εγγράψιμο.
εγγράψιμο. είναι
είναι 

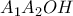 εγγράψιμο
εγγράψιμο


 παίρνουμε
παίρνουμε  που ισχύει αφού από
που ισχύει αφού από 
![xy+yz+xz\geq 3\sqrt[3]{x^2y^2z^2}\geq 3 xy+yz+xz\geq 3\sqrt[3]{x^2y^2z^2}\geq 3](/forum/ext/geomar/texintegr/latexrender/pictures/2c2e18ad8da507c79c1e06f5d29e0580.png)
 ,
, δέκα φυσικοί από το
δέκα φυσικοί από το ![\left [ 1,36 \right ] \left [ 1,36 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/992156fe4a767c6a8acf5a37e037ceef.png) για τους οποίους δεν ισχύει το ζητούμενο.
για τους οποίους δεν ισχύει το ζητούμενο. αναγκαστικά δεν θα υπάρχει ο
αναγκαστικά δεν θα υπάρχει ο  αφού εαν υπήρχε θα είχαμε
αφού εαν υπήρχε θα είχαμε  .
. αριθμοί άτοπο γιατί έτσι έχουμε τουλάχιστον
αριθμοί άτοπο γιατί έτσι έχουμε τουλάχιστον  αριθμούς .
αριθμούς . δέκα αριθμοί για τους οποίους δεν ισχύει το ζητούμενο. Προφανώς, το ζητούμενο είναι ισοδύναμο με το ότι υπάρχουν
δέκα αριθμοί για τους οποίους δεν ισχύει το ζητούμενο. Προφανώς, το ζητούμενο είναι ισοδύναμο με το ότι υπάρχουν  αριθμοί (διακεκριμένοι) ώστε η (θετική) διαφορά δύο εξ αυτών είναι ίση με την (θετική) διαφορά των άλλων δύο.
αριθμοί (διακεκριμένοι) ώστε η (θετική) διαφορά δύο εξ αυτών είναι ίση με την (θετική) διαφορά των άλλων δύο. για
για  .
. διαφορετικές δυνατές διαφορές δύο αριθμών από το
διαφορετικές δυνατές διαφορές δύο αριθμών από το  , και στο σύνολο των
, και στο σύνολο των  οπότε υπάρχουν δύο ίσες διαφορές.
οπότε υπάρχουν δύο ίσες διαφορές. .
. να είναι ίσα, WLOG τα
να είναι ίσα, WLOG τα  .
. διαφορές και
διαφορές και  δυνατές διαφορές.
δυνατές διαφορές. , υπάρχουν
, υπάρχουν  διαφορές και
διαφορές και  αν είναι ίσο με το
αν είναι ίσο με το  , εύκολα έχουμε άτοπο.
, εύκολα έχουμε άτοπο. δεν υφίσταται).
δεν υφίσταται). .
. με
με  και
και  και αρκεί να δείξω ότι
και αρκεί να δείξω ότι  και αφού
και αφού 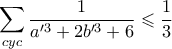 με
με  .
. και τα κυκλικά. Το ότι αυτές οι ανισότητες δίνουν το ζητούμενο είναι προφανές προσθέτοντας κυκλικά.
και τα κυκλικά. Το ότι αυτές οι ανισότητες δίνουν το ζητούμενο είναι προφανές προσθέτοντας κυκλικά. ή αλλιώς
ή αλλιώς  που ισχύει από ΑΜ-ΓΜ καθώς :
που ισχύει από ΑΜ-ΓΜ καθώς : και
και  .
. . Τότε τα
. Τότε τα  διαιρούν το
διαιρούν το  . Έστω
. Έστω  . Τότε
. Τότε  θετικοί ακέραιοι με
θετικοί ακέραιοι με  .
. . Επίσης πρέπει
. Επίσης πρέπει  αφού αλλιώς
αφού αλλιώς  .
. . Τότε
. Τότε 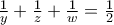 οπότε πρέπει
οπότε πρέπει  .
.  τότε
τότε  . Πρέπει
. Πρέπει  και
και  . Παίρνουμε τις λύσεις
. Παίρνουμε τις λύσεις  .
. τότε
τότε  . Πρέπει
. Πρέπει  και
και  . Παίρνουμε τις λύσεις
. Παίρνουμε τις λύσεις  .
.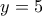 τότε
τότε  . Πρέπει
. Πρέπει  , άρα
, άρα  , το οποίο όμως δεν δίνει ακέραια λύση.
, το οποίο όμως δεν δίνει ακέραια λύση.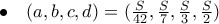 όπου
όπου  .
. όπου
όπου  .
. όπου
όπου  .
. όπου
όπου  .
. όπου
όπου  .
. όπου
όπου  .
.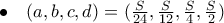 όπου
όπου  να είναι ίσος με τον
να είναι ίσος με τον 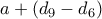 .
.  . Αν όμως είχαμε
. Αν όμως είχαμε  τότε αυτό δεν διορθώνεται και χρειάζεται κάποια παρόμοια ιδέα με του Ορέστη.
τότε αυτό δεν διορθώνεται και χρειάζεται κάποια παρόμοια ιδέα με του Ορέστη.