erxmer έγραψε:Έστω η συνεχής συνάρτηση

, παραγωγίσιμη στο

με

για κάθε

.
1) Να αποδειχθεί ότι

2) Να αποδειχθεί ότι η

είναι γνησίως αύξουσα στο

.
3) Να αποδειχθεί ότι η

είναι κοίλη στο

4) Nα λυθεί η εξίσωση

5) Να βρεθούν οι

για τους οποίους ισχύει:

6) Να υπολογισθεί το ολοκλήρωμα
![\displaystyle{I=\int_{8}^{64}\frac{x-1}{\sqrt[3]{x}{\mathrm f}(x)}{\mathrm d}x.} \displaystyle{I=\int_{8}^{64}\frac{x-1}{\sqrt[3]{x}{\mathrm f}(x)}{\mathrm d}x.}](/forum/ext/geomar/texintegr/latexrender/pictures/926ebe018fbf7402c5d8eb465252ccea.png)
Καλησπέρα. Μια προσπάθεια για τα 4 πρώτα...
1) Είναι

.
Για

έχουμε από Πόρισμα συνεπειών ΘΜΤ.:

Επίσης

,
επειδή

αφού η

είναι συνεχής.
Άρα

Επομένως

Συνεπώς

Ομοίως εργαζόμενοι συμπεραίνουμε

.
Τώρα λόγω συνέχειας και χρησιμοποιώντας τον κανόνα de L' Hospital έχουμε :

Άρα

2)Ισχύει

στο

όπου

με

Από πινακάκι φαίνεται εύκολα

Άρα

επομένως η

είναι γνησίως αύξουσα στο
![(0,1]. (0,1].](/forum/ext/geomar/texintegr/latexrender/pictures/48fcc93577a0c42f47ffe011f5bde061.png)
Επίσης

επομένως η

είναι γνησίως αύξουσα στο

Τώρα επειδή η

είναι συνεχής στο

συμπεραίνουμε ότι είναι και γνησίως αύξουσα στο διάστημα αυτό.
3) Ισχύει

,
όπου

με

και

Για

έχουμε

άρα

γνησίως αύξουσα στο
![(0,1] (0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/668c7b55a37300c330dcd565d9e076da.png)
, οπότε
για

είναι

Άρα

γνησίως φθίνουσα στο
![(0,1] (0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/668c7b55a37300c330dcd565d9e076da.png)
, οπότε για

είναι

Επίσης για

είναι

Άρα

επομένως η

κοίλη στο
![(0,1]. (0,1].](/forum/ext/geomar/texintegr/latexrender/pictures/48fcc93577a0c42f47ffe011f5bde061.png)
Ομοίως για

έχουμε

άρα

γνησίως φθίνουσα στο

, οπότε για

είναι

Άρα

γνησίως φθίνουσα στο

, οπότε για

είναι

Επίσης για

είναι

Άρα

επομένως η

κοίλη στο

Τελικά λόγω της συνέχειας η

κοίλη στο

4) Η εξίσωση



Ισχύει

αφού

και

Επιπλέον αφού η

είναι γνησίως αύξουσα έχουμε

Όμως

Επομένως η εξίσωση είναι αδύνατη.
Θα επανέλθω αύριο με τα υπόλοιπα.
Φιλικά
Σταμ. Γλάρος
 , παραγωγίσιμη στο
, παραγωγίσιμη στο  με
με  για κάθε
για κάθε  .
.
 είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο  .
. είναι κοίλη στο
είναι κοίλη στο 

 για τους οποίους ισχύει:
για τους οποίους ισχύει:
![\displaystyle{I=\int_{8}^{64}\frac{x-1}{\sqrt[3]{x}{\mathrm f}(x)}{\mathrm d}x.} \displaystyle{I=\int_{8}^{64}\frac{x-1}{\sqrt[3]{x}{\mathrm f}(x)}{\mathrm d}x.}](/forum/ext/geomar/texintegr/latexrender/pictures/926ebe018fbf7402c5d8eb465252ccea.png)


 .
. έχουμε από Πόρισμα συνεπειών ΘΜΤ.:
έχουμε από Πόρισμα συνεπειών ΘΜΤ.: 
 ,
, αφού η
αφού η  είναι συνεχής.
είναι συνεχής. Επομένως
Επομένως 

 .
.
 στο
στο  με
με 

 επομένως η
επομένως η ![(0,1]. (0,1].](/forum/ext/geomar/texintegr/latexrender/pictures/48fcc93577a0c42f47ffe011f5bde061.png)
 επομένως η
επομένως η 
 ,
, με
με  και
και 
 άρα
άρα  γνησίως αύξουσα στο
γνησίως αύξουσα στο ![(0,1] (0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/668c7b55a37300c330dcd565d9e076da.png) , οπότε
, οπότε είναι
είναι 
 γνησίως φθίνουσα στο
γνησίως φθίνουσα στο 

 επομένως η
επομένως η  έχουμε
έχουμε  άρα
άρα  , οπότε για
, οπότε για  είναι
είναι 

 επομένως η
επομένως η 

 αφού
αφού  και
και 


 και ισοδύναμα
και ισοδύναμα  άρα
άρα 
 είναι συνεχής συνάρτηση θα ισχύει ότι
είναι συνεχής συνάρτηση θα ισχύει ότι  έτσι
έτσι  και
και  επομένως
επομένως  ή
ή  ή
ή 
 θα είναι
θα είναι 

 με όπου
με όπου  το
το  ισχύει ότι
ισχύει ότι  άρα
άρα  για
για  και επειδή είναι συνεχής θα στο
και επειδή είναι συνεχής θα στο  είναι παραγωγίσιμη με
είναι παραγωγίσιμη με 
 είναι παραγωγίσιμη με
είναι παραγωγίσιμη με  όπως είδαμε και παραπάνω επομένως η
όπως είδαμε και παραπάνω επομένως η  είναι γνήσια φθίνουσα στο
είναι γνήσια φθίνουσα στο  και για
και για  επομένως η
επομένως η  επειδή
επειδή  και για
και για  επομένως η
επομένως η  επειδή
επειδή 

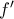 στο
στο 

 η
η  επομένως η
επομένως η  (1)
(1)  και επειδή λόγω μονοτονίας και συνέχειας το σύνολο τιμών της
και επειδή λόγω μονοτονίας και συνέχειας το σύνολο τιμών της  στο
στο  είναι
είναι  με
με 
 επομένως η (1) είναι αδύνατη.
επομένως η (1) είναι αδύνατη.


 το παραπάνω όριο είναι
το παραπάνω όριο είναι  .
.  οπότε
οπότε 
 Συνεπώς
Συνεπώς  και
και 
![\displaystyle{I=\int_{8}^{64}\frac{x-1}{\sqrt[3]{x}{\mathrm f}(x)}{\mathrm d}x} = \int_{8}^{64}\frac{x-1}{\sqrt[3]{x}\cdot \dfrac{x-1}{ln x}} dx = \int_{8}^{64}\frac{ln x}{\sqrt[3]{x}} dx = \displaystyle{I=\int_{8}^{64}\frac{x-1}{\sqrt[3]{x}{\mathrm f}(x)}{\mathrm d}x} = \int_{8}^{64}\frac{x-1}{\sqrt[3]{x}\cdot \dfrac{x-1}{ln x}} dx = \int_{8}^{64}\frac{ln x}{\sqrt[3]{x}} dx =](/forum/ext/geomar/texintegr/latexrender/pictures/b7bbd13cd805fa9e02287e876a96cea0.png)

 είναι
είναι 





