 . Να βρεθεί η εφαπτομένη της γραφικής παράστασης της
. Να βρεθεί η εφαπτομένη της γραφικής παράστασης της  που είναι παράλληλη στην ευθεία
που είναι παράλληλη στην ευθεία  καθώς και η ελάχιστη απόσταση των σημείων των γραφικών παραστάσεων των
καθώς και η ελάχιστη απόσταση των σημείων των γραφικών παραστάσεων των  , όπου
, όπου  .
.Από τον εξαίρετο "Οδηγό επανάληψης" των κ.Στεργίου, Νάκη.
Συντονιστής: Καρδαμίτσης Σπύρος
 . Να βρεθεί η εφαπτομένη της γραφικής παράστασης της
. Να βρεθεί η εφαπτομένη της γραφικής παράστασης της  που είναι παράλληλη στην ευθεία
που είναι παράλληλη στην ευθεία  καθώς και η ελάχιστη απόσταση των σημείων των γραφικών παραστάσεων των
καθώς και η ελάχιστη απόσταση των σημείων των γραφικών παραστάσεων των  , όπου
, όπου  .
. είναι κοίλη , ενώ η
είναι κοίλη , ενώ η  κυρτή . Παρατηρώ ότι οι εφαπτόμενες των
κυρτή . Παρατηρώ ότι οι εφαπτόμενες των  στα σημεία
στα σημεία αντίστοιχα είναι παράλληλες και απέχουν κατά
αντίστοιχα είναι παράλληλες και απέχουν κατά  αφού το
αφού το 
 των δύο καμπυλών
των δύο καμπυλών , συνεπώς η ελάχιστη απόσταση είναι
, συνεπώς η ελάχιστη απόσταση είναι  , σ'αυτή τη θέση .
, σ'αυτή τη θέση . .
. αντιστρέφεται και να βρεθεί το πεδίο ορισμού της
αντιστρέφεται και να βρεθεί το πεδίο ορισμού της 



α) Έστωpito έγραψε: ↑Σάβ Απρ 14, 2018 5:32 pmΕυχαριστώ κ.Θανάση!
Ένα επιπλέον ερώτημα( με υποερωτήματα) , πάλι από τον οδηγό:
Δίνεται η συνάρτηση.
α) Να δείξετε ότι ηαντιστρέφεται και να βρεθεί το πεδίο ορισμού της
β) Να λυθεί η εξίσωση
γ)Να βρεθούν, αν υπάρχουν , τα κοινά σημεία των
δ) Να λυθούν οι ανισώσεις
 ,
, . Τότε η
. Τότε η 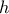 είναι γνησίως αύξουσα , άρα αντιστρέφεται .
είναι γνησίως αύξουσα , άρα αντιστρέφεται . 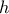 είναι το
είναι το  . Επομένως ορίζεται η
. Επομένως ορίζεται η  .
. είναι όλο το
είναι όλο το  .
. τότε είναι
τότε είναι  άρα δεν έχει ρίζες .
άρα δεν έχει ρίζες . τότε
τότε 
 είναι
είναι 

 είναι
είναι 
 . Άρα έχουν κοινό το
. Άρα έχουν κοινό το 
 η ανίσωση
η ανίσωση  είναι αδύνατη αφού
είναι αδύνατη αφού  και
και 
 και επειδή η
και επειδή η 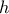 είναι γνησίως αύξουσα γίνεται
είναι γνησίως αύξουσα γίνεται 

 η ανίσωση
η ανίσωση  ισχύει , αφού
ισχύει , αφού  και
και 
 και επειδή η
και επειδή η 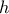 είναι γνησίως αύξουσα γίνεται
είναι γνησίως αύξουσα γίνεται 
 και τελικά για
και τελικά για 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης