Καλησπέρα σε όλους. Αφιερωμένη στους αγαπητούς συναδέλφους που έζησαν ως μαθητές τα χρόνια δίχως παραγώγους, μια τριγωνομετρικοαλγεβρική λύση (calculus free).(*)

- 25-11-2025 Τριγωνομετρία.jpg (23.45 KiB) Προβλήθηκε 43 φορές

, με οξεία γωνία.


Ζητώ το μέγιστο της παράστασης


Έχει μέγιστο όταν και το υπόρριζο έχει μέγιστο.
Αφού οι όροι έχουν σταθερό άθροισμα το γινόμενο είναι μέγιστο όταν

Τότε

(*)Φοβάμαι ότι έρχονται μέρες δίχως calculus, δίχως άλγεβρα, δίχως υπόλοιπο γεωμετρίας, δίχως τα μαθηματικά, όπως τα ξέρουμε, γενικώς. Όσοι δεν δώσατε προσοχή , ρίξτε μια ματιά στο νέο ύφος των θεμάτων της Α΄ Λυκείου
ΕΔΩ.
 Η άσκηση που ακολουθεί είναι Α' Ομάδας . Στην ακτίνα
Η άσκηση που ακολουθεί είναι Α' Ομάδας . Στην ακτίνα 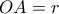 , του τεταρτοκυκλίου
, του τεταρτοκυκλίου  , κινείται
, κινείται  , στο οποίο φέρουμε κάθετη στην
, στο οποίο φέρουμε κάθετη στην  , η οποία τέμνει το τόξο στο σημείο
, η οποία τέμνει το τόξο στο σημείο  και στην προέκταση
και στην προέκταση  , ώστε :
, ώστε :  . Βρείτε το μέγιστο εμβαδόν του τριγώνου
. Βρείτε το μέγιστο εμβαδόν του τριγώνου  .
.

 Ο μηδενισμός της παραγώγου δίνει
Ο μηδενισμός της παραγώγου δίνει  και μέγιστο εμβαδόν
και μέγιστο εμβαδόν 
 , με οξεία γωνία.
, με οξεία γωνία.




