KARKAR έγραψε: ↑Σάβ Σεπ 21, 2024 10:57 am
Το σύνολο

περιέχει σε αύξουσα σειρά τους περιττούς πρώτους .
Εξετάστε αν αληθεύει ο ισχυρισμός : " Το άθροισμα τριών διαδοχικών στοιχείων του συνόλου

είναι
πρώτος ή γινόμενο δύο πρώτων " .
Δεν γνωρίζω αν το θέμα έχει λυθεί ή αν έχει καν τεθεί στο παρελθόν ...
Ενδιαφέρον αλλά δεν ισχύει, με αντιπαράδειγμα στα παρακάτω. Υποθέτω ότι θα μπορούσε κανείς να φτάξει ένα προγραμματάκι για να βρει το πρώτο αντιπαράδειγμα, αλλά σκέφτηκα αλλιώς. Πανηρά. Γράφω την σκέψη μου: Βρίσκω με χρήση απλών πινάκων πρώτων τρεις διαδοχικούς πρώτους που λήγουν σε

. Αυτό μας εξασφαλίζει ότι το άθροισμά τους, που λήγει σε

καθώς

, δεν είναι πρώτος ως πολλαπλάσιο του

. Διαιρώ το άθροισμα με το

για να βρώ τον άλλον παράγοντα και ελπίζω να μην είναι πρώτος. Μάλιστα έχω την πεποίθηση, πριν ξεκινήσω, ότι αργά ή γρήγορα δεν θα είναι πρώτος γιατί είναι μεγαλούτσικος αριθμός και άρα δύσκολα να μην έχει άλλον παράγοντα.
Πράγματι, με λίγες δοκιμές, έχοντας μπροστά μου πίνακα πρώτων και κομπιουτεράκι, βρίσκω

, οπότε τελειώσαμε.
 περιέχει σε αύξουσα σειρά τους περιττούς πρώτους .
περιέχει σε αύξουσα σειρά τους περιττούς πρώτους . είναι
είναι 
 . Αυτό μας εξασφαλίζει ότι το άθροισμά τους, που λήγει σε
. Αυτό μας εξασφαλίζει ότι το άθροισμά τους, που λήγει σε  καθώς
καθώς  , δεν είναι πρώτος ως πολλαπλάσιο του
, δεν είναι πρώτος ως πολλαπλάσιο του  , οπότε τελειώσαμε.
, οπότε τελειώσαμε.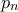 ο
ο  -οστός πρώτος, τότε έχουμε:
-οστός πρώτος, τότε έχουμε: και
και 