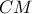 με την υποτείνουσα
με την υποτείνουσα  , ισούται με το μισό της
, ισούται με το μισό της 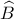 .
.Αν
 , υπολογίστε την
, υπολογίστε την  ( έστω και με προσέγγιση ) .
( έστω και με προσέγγιση ) .Αν γνωρίζουμε την
 , μπορούμε να υπολογίσουμε την
, μπορούμε να υπολογίσουμε την  ; (
; (  )
)Συντονιστής: Γιώργος Ρίζος
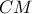 με την υποτείνουσα
με την υποτείνουσα  , ισούται με το μισό της
, ισούται με το μισό της 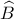 .
. , υπολογίστε την
, υπολογίστε την  ( έστω και με προσέγγιση ) .
( έστω και με προσέγγιση ) . , μπορούμε να υπολογίσουμε την
, μπορούμε να υπολογίσουμε την  ; (
; (  )
)Από τα προσεγγιστικά αποτελέσματα που δίδω στο σχήμα : αλλά και απο τον ορισμό :
 .
.Θέτω :
 ζητούμενο ) και
ζητούμενο ) και  ( παράμετροι ). Από το
( παράμετροι ). Από το 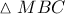 κι αφού η μια γωνία διπλάσιας της άλλης,
κι αφού η μια γωνία διπλάσιας της άλλης, . Από Π. Θ. στο
. Από Π. Θ. στο  ,
,  οπότε λόγω της
οπότε λόγω της  ,
,  που από το Π. Θ.
στο
που από το Π. Θ.
στο  δίδει :
δίδει :  .
. κατασκευάζεται . Επειδή εν γένει ( με
κατασκευάζεται . Επειδή εν γένει ( με  ) :
) : 
 τότε :
τότε :  .
. ( δεν το έχω ξαναδεί)
( δεν το έχω ξαναδεί)  ) .
) .Σε ότι αφορά την έκφραση της
 από την
από την  έχουμε :
έχουμε :
 δηλαδή προκύπτουν δύο λύσεις .
δηλαδή προκύπτουν δύο λύσεις .  όταν γνωρίζουμε το πέρας του τόξου
όταν γνωρίζουμε το πέρας του τόξου  .
. . Είναι
. Είναι  , ενώ
, ενώ  που έχει πέρας στο τρίτο τεταρτημόριο .
που έχει πέρας στο τρίτο τεταρτημόριο . . μετά αντικαθιστώ στην
. μετά αντικαθιστώ στην  κι έχω αυτό που θέλω .
κι έχω αυτό που θέλω .Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες