Ειδική χορδή

KARKAR · #1

: Ειδική χορδή.png (12.57 KiB) Προβλήθηκε 109 φορές

$\bigstar$ Στον κύκλο (O)

να βρείτε χορδή A'B'

, η οποία να είναι ίση και παράλληλη με το τμήμα

.

#2

KARKAR έγραψε: ↑
Δευ Νοέμ 24, 2025 9:56 am
Ειδική χορδή.png $\bigstar$ Στον κύκλο να βρείτε χορδή , η οποία να είναι ίση και παράλληλη με το τμήμα .

Γεωμετρική Κατασκευή

1. Τοποθετώ στον δεδομένο κύκλο $\left( {O,R} \right)$ , χορδή μήκους AB = d

. Προς τούτο γράφω με κέντρο τυχαίο σημείο,

του

κύκλου , τον κύκλο $\left( {T,d} \right)$ που τέμνει σε δύο σημεία τον $\left( {O,R} \right)$ κι έστω το ένα απ’ αυτά, ας πούμε,

.

2. Αν

το μέσο της

, θεωρό νέο ομόκεντρο κύκλο $\Omega$ , κέντρου

κι ακτίνας , r = OM

.

Προφανώς η TZ = d

. είναι χορδή του $\left( {O,R} \right)$ κι εφάπτεται στο κύκλο $\Omega$ στο

. Όμως και κάθε χορδή του $\left( {O,R} \right)$ που εφάπτεται

Στον $\Omega$ θα έχει μήκος

.
.

: Ειδική χορδή.png (35.94 KiB) Προβλήθηκε 68 φορές

.
3. Μετά απ αυτά από το

φέρνω κάθετη στη σταθερή ευθεία

και θα τέμνει τον $\Omega$ στα $E\,\,\kappa \alpha \iota \,\,H$ .

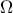4. οι χορδές του $\left( {O,R} \right)$ που εφάπτονται στον $\Omega$ , στα σημεία του , $E\,\,\kappa \alpha \iota \,\,H$ είναι αυτές που θέλω αφού :

5. Αν τις ονομάσω , $A'B'\,\,\,\,\kappa \alpha \iota \,\,\,\,A''B''\,$ θα είναι : $A'B'// = AB = d\,\,\,\kappa \alpha \iota \,\,A''B''// = AB = d\,$

Παρατήρηση .

Ο υπολογισμός των συντεταγμένων των πιο πάνω χορδών δεν είναι δύσκολος αν ληφθεί με βάσει τις κατασκευές τους.

Θα ψάξω όμως και ανεξάρτητη απλή λύση, εντός του φακέλου που έχει τεθεί η άσκηση .

#3

KARKAR έγραψε: ↑
Δευ Νοέμ 24, 2025 9:56 am
Ειδική χορδή.png $\bigstar$ Στον κύκλο να βρείτε χορδή , η οποία να είναι ίση και παράλληλη με το τμήμα .

Θέτω $\displaystyle A'\left( {a,\sqrt {9 - {a^2}} } \right),B'\left( {b, - \sqrt {9 - {b^2}} } \right)$

: Ειδική χορδή.png (14.7 KiB) Προβλήθηκε 56 φορές

$\displaystyle \overrightarrow {A'B'} = \overrightarrow {AB} \Leftrightarrow b - a = 5,\sqrt {9 - {a^2}} + \sqrt {9 - {b^2}} = 3,$ απ' όπου παίρνω

$\displaystyle a = \frac{{ - 85 \pm 3\sqrt {17} }}{{34}}.$ Υπάρχουν δύο χορδές A'B', A''B'',

με $\displaystyle A'\left( {\frac{{ - 85 - 3\sqrt {17} }}{{34}},\sqrt {\frac{{178 - 30\sqrt {17} }}{{68}}} } \right),$

$\displaystyle A''\left( {\frac{{ - 85 + 3\sqrt {17} }}{{34}},\sqrt {\frac{{178 + 30\sqrt {17} }}{{68}}} } \right).$ Ομοίως βρίσκω και τα σημεία B', B''.

duamba · #4

Καλησπέρα σε όλους,

Ακόμα μία κατασκευαστική λύση:

: eidiki-chordi.png (41.96 KiB) Προβλήθηκε 46 φορές

Βρίσκω το συμμετρικό A''B''

του

ώς προς το κέντρο

και συμπληρώνω το παραλληλόγραμμο A,B,A'',B''

.
Φέρνω παράλληλη της

απο το κέντρο

που τέμνει τον κύκλο στα C,D

και τις

,

στα

.
Τέλος απο τα A''', B'''

φέρνω κάθετες στην

για να βρώ τα ζητούμενα A',B'

.

Ειδική χορδή

Ειδική χορδή

Re: Ειδική χορδή

Re: Ειδική χορδή

Re: Ειδική χορδή

Μέλη σε σύνδεση