Αγαπητοί φίλοι της Γεωμετρίας, φίλοι μου.
Σ’ αυτό εδώ τον χώρο, θα σας παρουσιάζουμε στο εξής, ενδιαφέρουσες, κατά την γνώμη μας πρωτοεμφανιζόμενες Γενικεύσεις, Επεκτάσεις, Αποδείξεις γνωστών Προτάσεων - Προβλήματα- γ.τ. Γεωμετρίας, τις οποίες έχουμε επινοήσει κατά το παρελθόν και τις οποίες δεν είχαμε συναντήσει μέχρι τότε, στη γνωστή μας βιβλιογραφία, άσχετα αν εκ των υστέρων έχουμε συναντήσει κάποιες απ’ αυτές. .
Για όλα αυτά θα θέλαμε να μας γνωρίζετε συγκεκριμένα αν τα έχετε συναντήσει, που, πότε, προκειμένου να μάθουμε την αλήθεια και να κάνετε την σχετική καλοπροαίρετη κριτική σας.
Εξυπακούεται ότι, οι παραπάνω Προτάσεις, Προβλήματα,-γ.τ. Γεωμετρίας, μπορεί να είναι πολύ δύσκολα μέχρι και πολύ απλά.
Στόχος μας είναι απλά και μόνο να δημοσιεύσουμε στο mathematica όσο το δυνατό περισσότερες Γενικεύσεις, Επεκτάσεις Αποδείξεις γνωστών Προτάσεων, Προβλήματα, γ.τ. Γεωμετρίας, μπορέσουμε και λιγότερο η συμμετοχή.
Οι ενδιαφερόμενοι μελετητές τούτων είναι δυνατό να δίνουν τις δικές τους Επεκτάσεις- Γενικεύσεις- Αποδείξεις και τα δικά τους σχόλια.
Αγαπητοί φίλοι σημειώνω εδώ ότι καλό είναι να γνωρίζετε ότι όπου, στα κείμενά μου που ακολουθούν, υπάρχουν οι παρακάτω μορφές συμβολισμών:
1α(ν), 1β(ν), 1γ(ν), 1δ(ν), 1ε(ν), 1ζ(ν), 2α(ν), 2β(ν), 2γ(ν), 2δ(ν), 2ε(ν), 2ζ(ν), 4 η(ν). 5θ(ν), 6ι(ν), 7ι(ν), 8ι(ν), 9ι(ν). 10ι(ν). 11(ν), 12(ν) (Όπου ν=1, 2, 3, 4, 5,……),
σημαίνει ότι αυτοί αποτελούν νέες Προτάσεις- Προβλήματα - γ.τ, κτλ. του γράφοντος, τις οποίες πρωτοεμφάνισα στα βιβλία μου ¨Νέα Στοιχεία Γεωμετρίας¨, κτλ, αποτελούν δε μέρος από τις 4.500 περίπου που έχω επινοήσει κατά το παρελθόν.
Μετά τα παραπάνω, κάνουμε την αρχή με την παρακάτω,
Γενίκευση B28:
«Τριγώνου
 , όλες οι πλευρές του τέμνονται από κύκλο
, όλες οι πλευρές του τέμνονται από κύκλο  ή έλλειψη, στα ζεύγη των σημείων:
ή έλλειψη, στα ζεύγη των σημείων:  ,
,  ,
,  .
. Αν είναι:
 ,
,  ,
,  ,
, ,
,  ,
,  ,
, τότε θα είναι:
 και
και  .
./u]
Αγαπητοί φίλοι, για την παραπάνω Πρόταση, περιμένουμε τις απαντήσεις σας, πάντα μέσα στο παραπάνω αναφερόμενο πνεύμα.
Δική μας απόδειξη θα δοθεί σε εύλογο χρονικό διάστημα.
Φιλικά
Νίκος Κυριαζής.

 .
.  (μαύρες στο σχήμα) του τριγώνου
(μαύρες στο σχήμα) του τριγώνου  συγκλίνουν στο
συγκλίνουν στο  . Η υπερβολή (κόκκινη στο σχήμα) διέρχεται από τα
. Η υπερβολή (κόκκινη στο σχήμα) διέρχεται από τα 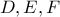 και επανατέμνει το τρίγωνο στα σημεία
και επανατέμνει το τρίγωνο στα σημεία 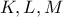 . Τότε οι σεβιανές
. Τότε οι σεβιανές  (πράσινες στο σχήμα) συγκλίνουν και αυτές, στο
(πράσινες στο σχήμα) συγκλίνουν και αυτές, στο  .
.  μέχρι να τμήσουν τις απέναντι πλευρές στα
μέχρι να τμήσουν τις απέναντι πλευρές στα  .
.  είναι συγκλίνουσα δέσμη, έχουμε από Ceva
είναι συγκλίνουσα δέσμη, έχουμε από Ceva 
 και
και  έχουμε
έχουμε  και
και 

 και κυκλικά, άλλες δύο. Κάνοντας τις απλοποιήσεις (σημείωσα με κόκκινο την προηγούμενη περίπτωση) μένει
και κυκλικά, άλλες δύο. Κάνοντας τις απλοποιήσεις (σημείωσα με κόκκινο την προηγούμενη περίπτωση) μένει 
 (οι κόκκινες γραμμές) συγκλίνουν. Όμοια η δεύτερη τριάδα.
(οι κόκκινες γραμμές) συγκλίνουν. Όμοια η δεύτερη τριάδα.  . Αλλά πόσο καινούργια και πόσο πρωτότυπη είναι; Λέω λοιπόν, αν διπλασιάσεις το σχήμα του Garfield παίρνεις το δεξί σχήμα, στο οποίο και πάλι, ο υπολογισμός του εμβαδού με δύο διαφορετικούς τρόπους, δίνει την ίδια σχέση. Νέα απόδειξη; Ούτε συζήτηση! Η απόδειξη του Garfield είναι απλά η δεξιά μόνο που κόψαμε το σχήμα σε δύο ίσα μέρη με την κόκκινη γραμμή. ΤΙΠΟΤΑ ΑΛΛΟ.
. Αλλά πόσο καινούργια και πόσο πρωτότυπη είναι; Λέω λοιπόν, αν διπλασιάσεις το σχήμα του Garfield παίρνεις το δεξί σχήμα, στο οποίο και πάλι, ο υπολογισμός του εμβαδού με δύο διαφορετικούς τρόπους, δίνει την ίδια σχέση. Νέα απόδειξη; Ούτε συζήτηση! Η απόδειξη του Garfield είναι απλά η δεξιά μόνο που κόψαμε το σχήμα σε δύο ίσα μέρη με την κόκκινη γραμμή. ΤΙΠΟΤΑ ΑΛΛΟ.  και
και  που συγκλίνουν στα σημεία
που συγκλίνουν στα σημεία  , αντίστοιχα. Ορίζουμε
, αντίστοιχα. Ορίζουμε  τα σημεία τομής των
τα σημεία τομής των  ,
,  και
και  αντίστοιχα. Τότε οι ευθείες
αντίστοιχα. Τότε οι ευθείες  συγκλίνουν (κόκκινες στο σχήμα).
συγκλίνουν (κόκκινες στο σχήμα). τέμνουν τις απέναντι πλευρές στα
τέμνουν τις απέναντι πλευρές στα  έχουμε
έχουμε  .
. και
και  έχουμε
έχουμε  και
και .
.
 και
και 
 παραπάνω (για παράδειγμα η πρώτη είναι σημειωμένη με κόκκινο) παίρνουμε
παραπάνω (για παράδειγμα η πρώτη είναι σημειωμένη με κόκκινο) παίρνουμε  , από όπου η ζητούμενη σύγκλιση.
, από όπου η ζητούμενη σύγκλιση.  στην προέκταση της βάσης. Από το
στην προέκταση της βάσης. Από το  που τέμνουν τις πλευρές
που τέμνουν τις πλευρές  στα
στα 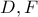 και
και  , αντίστοιχα. Από σημείο
, αντίστοιχα. Από σημείο  της βάσης φένουμε τα
της βάσης φένουμε τα  που τέμνουν την
που τέμνουν την  στα
στα  , αντίστοιχα. Τότε οι
, αντίστοιχα. Τότε οι  συγκλίνουν (κόκκινες στο σχήμα).
συγκλίνουν (κόκκινες στο σχήμα).