 τέτοιες, ώστε
τέτοιες, ώστε  για κάθε
για κάθε  .
.Συντονιστές: achilleas, emouroukos, silouan
 τέτοιες, ώστε
τέτοιες, ώστε  για κάθε
για κάθε  .
. η δοθείσα σχέση.
η δοθείσα σχέση.  δίνει
δίνει  , οπότε
, οπότε  .
.  τέτοιο ώστε
τέτοιο ώστε  , τότε η
, τότε η  δίνει
δίνει  , οπότε
, οπότε  για κάθε
για κάθε  . Η μηδενική συνάρτηση αποτελεί λύση της δοθείσας εξίσωσης.
. Η μηδενική συνάρτηση αποτελεί λύση της δοθείσας εξίσωσης. για κάθε
για κάθε  . Αν
. Αν  , τότε η
, τότε η  δίνει
δίνει , οπότε
, οπότε 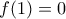 , άτοπο. Άρα
, άτοπο. Άρα  . (*)
. (*) δίνει
δίνει  . (1)
. (1) και
και  (για
(για  ), και χρησιμοποιώντας την (*) και την (1) παίρνουμε
), και χρησιμοποιώντας την (*) και την (1) παίρνουμε , (2)
, (2) δίνει
δίνει  (3).
(3).  είναι επί. Έστω
είναι επί. Έστω  και
και  τέτοιο ώστε
τέτοιο ώστε  , οπότε από την (3) είναι
, οπότε από την (3) είναι  . Τότε η (2) δίνει
. Τότε η (2) δίνει ,
,  είναι προσθετική. Από την τελευταία και την
είναι προσθετική. Από την τελευταία και την  παίρνουμε
παίρνουμε ,
,  , δηλ.
, δηλ.  ,
,  είναι πολλαπλασιαστική.
είναι πολλαπλασιαστική.  είναι προσθετική και πολλαπλασιαστική. Άρα, η
είναι προσθετική και πολλαπλασιαστική. Άρα, η  σε αυτη την περίπτωση είναι η ταυτοτική, η οποία ικανοποιεί τη δοθείσα σχέση. Συνεπώς, οι λύσεις είναι η μηδενική και η ταυτοτική.
σε αυτη την περίπτωση είναι η ταυτοτική, η οποία ικανοποιεί τη δοθείσα σχέση. Συνεπώς, οι λύσεις είναι η μηδενική και η ταυτοτική. , θα μπορούσαμε να έχουμε οποιοδήποτε θετικό περιττό εκθέτη
, θα μπορούσαμε να έχουμε οποιοδήποτε θετικό περιττό εκθέτη  , δηλ.
, δηλ. 
 .
. Ναι, Δημήτρη, συμφωνώ.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες