Συναρτησιακή στο R+

#1

Να προσδιορίσετε όλες τις συναρτήσεις $f : \mathbb{R}^+ \to \mathbb{R}^+$ τέτοιες ώστε $f(x^{2}f(x)+f(y)) = (f(x))^{3}+y ,$ για κάθε $x,y \in \Bbb{R}^+.$

Ορέστης Λιγνός · #2

socrates έγραψε: ↑
Παρ Μάιος 06, 2022 8:10 pm
Να προσδιορίσετε όλες τις συναρτήσεις $f : \mathbb{R}^+ \to \mathbb{R}^+$ τέτοιες ώστε $f(x^{2}f(x)+f(y)) = (f(x))^{3}+y ,$ για κάθε $x,y \in \Bbb{R}^+.$

Καλή!

Αρχίζουμε με κάποιους Ισχυρισμούς:

Ισχυρισμός 1: Η

είναι 1-1.
Απόδειξη: Άμεσο από την αρχική καθώς αν f(y_1)=f(y_2)

για κάποια y_1,y_2>0

, τότε

άρα

όπως θέλαμε $\blacksquare$

Ισχυρισμός 2: Υπάρχει σταθερά N>0

ώστε η

να είναι επί στο $(N,+\infty)$ .
Απόδειξη: Πράγματι, η αρχική για x=1

και

δίνει ότι

, άρα η

είναι επί στο $(f^3(1),+\infty)$ $\blacksquare$

Ισχυρισμός 3: Υπάρχει σταθερά

τέτοια, ώστε f(f^3(x))=x^2f(x)+c

για κάθε

.
Απόδειξη: Πράγματι, είναι

f(x^2f(x)+f(f^3(y)))=f^3(x)+f^3(y)=f(y^2f(y)+f(f^3(x))),

και αφού από τον Ισχυρισμό 1 η

είναι 1-1, προκύπτει ότι x^2f(x)+f(f^3(y))=y^2f(y)+f(f^3(x)),

δηλαδή η

είναι σταθερή, όπως θέλαμε $\blacksquare$

Στο πρόβλημα τώρα, έστω τυχαίο z>0

. Είναι,

συνεπώς αφού η

είναι 1-1,

y^2f(y)+f(f^3(x)+z)=x^2f(x)+f(f(f^3(y)+z),

η οποία λόγω του Ισχυρισμού 3 γράφεται ως

f(f^3(x)+z)+f(f^3(y))=f(f^3(y)+z)+f(f^3(x))

Από τον Ισχυρισμό 2 τώρα, αφού η

είναι τελικά επί, υπάρχει M>0

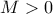τέτοιο, ώστε

f(x+z)+f(y)=f(y+z)+f(x)

, για κάθε x,y>M

. Έστω

και

, οπότε τελικά

f(x+z+M)+f(y)=f(y+z+M)+f(x),

για κάθε

.

Άρα, με z:=x+z

, προκύπτει

f(2x+z+M)+f(y)=f(x+y+z+M)+f(x)

(1)

και με x:=x+y

, προκύπτει

f(x+y+z+M)+f(y)=f(y+z+M)+f(x+y)

(2)

Συνδυάζοντας τις (1) και (2) προκύπτει ότι

f(x)-f(y)=f(2x+z+M)+f(y)-f(y+z+M)-f(x+y),

δηλαδή

.

Όμως, f(2x+z+M)-f(y+z+M)=f(2x)-f(y),

συνεπώς

, για κάθε x,y>0

.

Άρα,

δηλαδή υπάρχει σταθερά

τέτοια, ώστε f(2x)=2f(x)+c'

, για κάθε x>0

.

Άρα,

. Έστω

, οπότε εύκολα g(x+y)=g(x)+g(y)

. Οπότε η

είναι Cauchy και αφού g(x)=f(x)-c'>-c'

, είναι κάτω φραγμένη, άρα γραμμική.

Οπότε και η

είναι γραμμική και εύκολα πλέον ελέγχουμε ότι είναι η ταυτοτική.

Τελικά, μόνη λύση η $f \equiv \rm id$ .

#3

Συναρτησιακή στο R+

Συναρτησιακή στο R+

Re: Συναρτησιακή στο R+

Re: Συναρτησιακή στο R+

Μέλη σε σύνδεση