Δίνονται δύο κύκλοι
 τεμνόμενοι ορθογωνίως και έστω
τεμνόμενοι ορθογωνίως και έστω  μία κοινή εφαπτομένη τους με
μία κοινή εφαπτομένη τους με  Φέρνουμε τις εφαπτόμενες
Φέρνουμε τις εφαπτόμενες  των κύκλων
των κύκλων  αντιστοίχως και έστω το σημείο
αντιστοίχως και έστω το σημείο  Αποδείξτε ότι
Αποδείξτε ότι  Κώστας Βήττας.
Κώστας Βήττας.ΥΓ. Είναι προφανές ότι στο τρίγωνο
 του σχήματος, ισχύει
του σχήματος, ισχύει  . Αποδεικνύεται ότι αληθεύει και η αντίστροφη πρόταση. Εάν σε ένα δοσμένο τρίγωνο
. Αποδεικνύεται ότι αληθεύει και η αντίστροφη πρόταση. Εάν σε ένα δοσμένο τρίγωνο  ισχύει η
ισχύει η  τότε οι κύκλοι έστω
τότε οι κύκλοι έστω  που εφάπτονται των πλευρών των γωνιών
που εφάπτονται των πλευρών των γωνιών  στα σημεία
στα σημεία  αντιστοίχως, τέμνονται ορθογωνίως.
αντιστοίχως, τέμνονται ορθογωνίως.
 το έγκεντρο του
το έγκεντρο του  ,
,  ο σημείο επαφής της
ο σημείο επαφής της  .
. ,
, 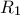 ,
,  οι ακτίνες των κύκλων
οι ακτίνες των κύκλων  ,
,  αντίστοιχα, και
αντίστοιχα, και  .
.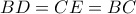 .
.
 και λόγου
και λόγου  μετασχηματίζει τον κύκλο
μετασχηματίζει τον κύκλο  στον εγγεγραμμένο κύκλο
στον εγγεγραμμένο κύκλο  (σημείο επαφής της
(σημείο επαφής της  με τον
με τον 
 .
. (όπου
(όπου  ,
,  ,
,  οι πλευρές του τριγώνου και
οι πλευρές του τριγώνου και 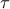 η ημιπερίμετρός του).
η ημιπερίμετρός του). 
 και λόγου
και λόγου  μετασχηματίζει τον κύκλο
μετασχηματίζει τον κύκλο  , όπου
, όπου  το σημείο επαφής της
το σημείο επαφής της  με τον
με τον  και
και  έχουμε
έχουμε 
 και
και  έχουμε
έχουμε 
 φέρουμε παράλληλο της
φέρουμε παράλληλο της  στο
στο  . Από το ορθογώνιο τρίγωνο
. Από το ορθογώνιο τρίγωνο  :
:
 (οι κύκλοι
(οι κύκλοι  λόγω των
λόγω των  και
και  γίνεται
γίνεται 
 ,
,
 .
.