Μια προσπάθεια:
Θα δείξουμε αρχικά ότι ισχύει

(αναρωτιέμαι αν, που σίγουρα, υπάρχουν κομψότερες λύσεις για αυτό γιατί μου φαίνεται και πιο γενικό πρόβλημα).
Επειδή

, σύμφωνα με γνωστό λήμμα αρκεί να δείξουμε ότι

.
Από τον νόμο των ημιτόνων έχουμε διαδοχικά:

.
Από την άλλη:

.
Επειδή τα

και

είναι όμοια θα είναι

,

άρα

.
Όμως:

Άρα:

, οπότε τελικά

, όπως θέλαμε.
Επομένως

άρα

.
Άρα, αφού τα τρίγωνα

και

είναι όμοια θα ισχύει

, άρα

.
Για το άλλο σκέλος,
εύκολα παρατηρούμε ότι τα τρίγωνα

και τα

είναι ίσα (ΠΓΠ), οπότε

.
Επίσης με μεταφορές γωνιών

και άρα

Οι γωνίες δηλαδή

και

είναι ίσες και βαίνουν στα ίσα τόξα

των κύκλων

αντίστοιχα, άρα οι κύκλοι είναι ίσοι.
Άρα

και

(ίσα τόξα
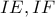
), οπότε

και άρα

.
Επειδή η
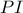
διχοτομεί τη γωνία

του ισοσκελούς

θα είναι κάθετη στην

.
Όμοια η

είναι κάθετη στην

, άρα η

είναι κάθετη στην

.
Όμως

, επομένως

και

.
Tελικά

.
 με έκκεντρο
με έκκεντρο  η εσωτερική διχοτόμος του
η εσωτερική διχοτόμος του  το ύψος του
το ύψος του  και
και  η διάμετρος του περιγεγραμμένου κύκλου του. Ο κύκλος
η διάμετρος του περιγεγραμμένου κύκλου του. Ο κύκλος  επανατέμνει την πλευρά
επανατέμνει την πλευρά  στο σημείο
στο σημείο  και ο κύκλος
και ο κύκλος  επανατέμνει την πλευρά
επανατέμνει την πλευρά  στο σημείο
στο σημείο 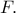 Οι περιγεγραμμένοι κύκλοι των τριγώνων
Οι περιγεγραμμένοι κύκλοι των τριγώνων  τέμνονται για δεύτερη φορά στο σημείο
τέμνονται για δεύτερη φορά στο σημείο  και ο περιγεγραμμένος κύκλος του τριγώνου
και ο περιγεγραμμένος κύκλος του τριγώνου  επανατέμνει το ύψος
επανατέμνει το ύψος  στο σημείο
στο σημείο  ενώ οι περιγεγραμμένοι κύκλοι των τριγώνων
ενώ οι περιγεγραμμένοι κύκλοι των τριγώνων  τέμνονται για δεύτερη φορά στο σημείο
τέμνονται για δεύτερη φορά στο σημείο  και ο περιγεγραμμένος κύκλος του τριγώνου
και ο περιγεγραμμένος κύκλος του τριγώνου  επανατέμνει την πλευρά
επανατέμνει την πλευρά  στο σημείο
στο σημείο  Να αποδείξετε ότι οι ευθείες
Να αποδείξετε ότι οι ευθείες  και
και  είναι κάθετες.
είναι κάθετες.
 (αναρωτιέμαι αν, που σίγουρα, υπάρχουν κομψότερες λύσεις για αυτό γιατί μου φαίνεται και πιο γενικό πρόβλημα).
(αναρωτιέμαι αν, που σίγουρα, υπάρχουν κομψότερες λύσεις για αυτό γιατί μου φαίνεται και πιο γενικό πρόβλημα).  , σύμφωνα με γνωστό λήμμα αρκεί να δείξουμε ότι
, σύμφωνα με γνωστό λήμμα αρκεί να δείξουμε ότι  .
. .
. .
. και
και  είναι όμοια θα είναι
είναι όμοια θα είναι  ,
,  άρα
άρα  .
.
 , οπότε τελικά
, οπότε τελικά  άρα
άρα  .
. και
και  είναι όμοια θα ισχύει
είναι όμοια θα ισχύει  , άρα
, άρα  .
. και τα
και τα  είναι ίσα (ΠΓΠ), οπότε
είναι ίσα (ΠΓΠ), οπότε  .
. και άρα
και άρα 
 και
και  είναι ίσες και βαίνουν στα ίσα τόξα
είναι ίσες και βαίνουν στα ίσα τόξα  των κύκλων
των κύκλων  αντίστοιχα, άρα οι κύκλοι είναι ίσοι.
αντίστοιχα, άρα οι κύκλοι είναι ίσοι. και
και  (ίσα τόξα
(ίσα τόξα 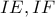 ), οπότε
), οπότε  και άρα
και άρα  .
.  διχοτομεί τη γωνία
διχοτομεί τη γωνία  του ισοσκελούς
του ισοσκελούς  θα είναι κάθετη στην
θα είναι κάθετη στην  .
.  είναι κάθετη στην
είναι κάθετη στην  , επομένως
, επομένως  και
και  .
. .
.