Ίσες γωνίες , διπλάσια βάση

KARKAR · #1

: Ίσες γωνίες , διπλάσια βάση.png (14.82 KiB) Προβλήθηκε 392 φορές

Τα σημεία S , T

της πλευράς

του ορθογωνίου τριγώνου ABC

είναι τέτοια , ώστε τα τμήματα BS , BT

να τριχοτομούν την γωνία $\hat{B}$ . Αν είναι : TC=2AS

, μπορούμε άραγε να υπολογίσουμε την γωνία $\hat{B}$ ;

S.E.Louridas · #2

KARKAR έγραψε: ↑
Πέμ Δεκ 26, 2024 8:49 pm
Τα σημεία της πλευράς του ορθογωνίου τριγώνου είναι τέτοια , ώστε τα τμήματα
να τριχοτομούν την γωνία $\hat{B}$ . Αν είναι : , μπορούμε άραγε να υπολογίσουμε την γωνία $\hat{B}$ ;

Για τα χρόνια πολλά μία προσπάθεια;

Αν

είναι το συμμετρικό του

ως προς

και

το κέντρο του περιεγραμμένου κύκλου στο τρίγωνο BTC,

τότε ισχύει

$SF = 2AS \Rightarrow SF = TC \Rightarrow \vartriangle BSF = \vartriangle KTC \Rightarrow BK\parallel AC,$ οπότε προκύπτουν τα εξής:

$BF = KT = KC = BK\mathop \Rightarrow \limits^{\angle CBK = x} \angle BCT = x \Rightarrow \angle BKF = \angle KFB = 2x \Rightarrow x = {36^ \circ },$

άρα τελικά $\angle B = {54^ \circ }.$ Απλά να προσθέσω βέβαια ότι λόγω της παραλληλίας των BK, AT

και του ότι KB=KT

η

προκύπτει διχοτόμος της γωνίας $\angle KTA$ που σημαίνει ότι η

διέρχεται από το

: GEO.png (43.56 KiB) Προβλήθηκε 375 φορές

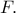edit: Προσθήκη επεξήγησης

#3

KARKAR έγραψε: ↑
Πέμ Δεκ 26, 2024 8:49 pm
Τα σημεία της πλευράς του ορθογωνίου τριγώνου είναι τέτοια , ώστε τα τμήματα

να τριχοτομούν την γωνία $\hat{B}$ . Αν είναι : , μπορούμε άραγε να υπολογίσουμε την γωνία $\hat{B}$ ;

Ενδιαφέρον: B=54^o

Πράγματι, με AS=x, ST=y, TC=2AS=2x

έχουμε από τα ορθογώνια τρίγωνα BAS, BAT, BAC

(παίρνοντας χωρίς βλάβη c=1

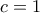και γράφοντας B/3=u

) ότι

$\tan u= x, \, \tan 2u = x+y, \tan 3u= 3x+y$ .

Έπεται αμέσως ότι $\boxed {\tan 3u= \tan 2u + 2 \tan u}$ (*)

.

Γράφοντας $\tan u = t, \, \tan 2u = \dfrac {2t}{1-t^2} , \, \tan 3u = \dfrac {3t-t^3}{1-3t^2}$ στην παραπάνω, μετά τις απλοποιήσεις δίνει

$\boxed {5t^4 -10t^2+1=0}$ . Εύκολα ελέγχουμε ότι έχει ρίζα την $\boxed {t =\dfrac { \sqrt {25-10\sqrt 5}}{5}}$ την οποία αναγνωρίζουμε ως $\boxed {t= \tan 18}$ (βλέπε π.χ. εδώ)

Συνοψίζοντας, είναι u=18^o

από όπου

.

Επίσης έκανα έλεγχο με κομπιουτεράκι ότι η (*)

ικανοποιείται από την u=18^o

.

Yποθέτω ότι τώρα που ξέρουμε ότι B=54^o

, υπάρχει ευκολότερος (γεωμετρικός;) τρόπος να συνάγουμε το ζητούμενο.

Edit: Με πρόλαβε ο Σωτήρης, με πολλή ωραία λύση, όσο έγραφα (που μου πήρε άπειρο χρόνο δακτυλογράφησης)

#4

KARKAR έγραψε: ↑
Πέμ Δεκ 26, 2024 8:49 pm
Ίσες γωνίες , διπλάσια βάση.pngΤα σημεία της πλευράς του ορθογωνίου τριγώνου είναι τέτοια , ώστε τα τμήματα

να τριχοτομούν την γωνία $\hat{B}$ . Αν είναι : , μπορούμε άραγε να υπολογίσουμε την γωνία $\hat{B}$ ;

Περιγραφικά, αποφεύγοντας τις πολλές πράξεις. Με θεώρημα διχοτόμων

στα BAT, BSC

και με Πυθαγόρειο βρίσκω $\displaystyle x = \frac{{2{b^2} - {a^2}}}{{2b}},BS = \frac{{{a^2}}}{{2b}},BT = \frac{{ac}}{b}$

: Ίσες γωνίες διπλάσια βάση.png (11.69 KiB) Προβλήθηκε 323 φορές

Στη συνέχεια από $\displaystyle \frac{x}{{b - 3x}} = \frac{c}{{BT}}$ με αντικατάσταση των x, BT

καταλήγω στην εξίσωση:

$\displaystyle 4{b^3} + 2a{b^2} - 3{a^2}b - {a^3} = 0 \Leftrightarrow 4{\sin ^3}B + 2{\sin ^2}B - 3\sin B - 1 = 0 \Leftrightarrow$

$\displaystyle (\sin B + 1)(4{\sin ^2}B - 2\sin B - 1) = 0,$ απ' όπου παίρνω τη δεκτή ρίζα

$\displaystyle \sin B = \frac{{\sqrt 5 + 1}}{4}$ και αφού η $\widehat B$ είναι οξεία, $\boxed{\widehat B=54^o}$

Μιχάλης Τσουρακάκης · #5

KARKAR έγραψε: ↑
Πέμ Δεκ 26, 2024 8:49 pm
Ίσες γωνίες , διπλάσια βάση.pngΤα σημεία της πλευράς του ορθογωνίου τριγώνου είναι τέτοια , ώστε τα τμήματα

να τριχοτομούν την γωνία $\hat{B}$ . Αν είναι : , μπορούμε άραγε να υπολογίσουμε την γωνία $\hat{B}$ ;

Με

συμμετρικό του

ως προς

,η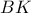

διχοτομεί την γωνία

άρα

Επειδή

,θα είναι $SM=MT \Rightarrow \angle QKB=2 \theta \Rightarrow BN//KQ \Rightarrow BNKQ$

ισοσκελές τραπέζιο,όπως και το BQCK

Ακόμη $\angle BKN= \angle MKN- \theta = \angle MKC- \theta = \angle QKC \Rightarrow BQCN$ ισοσκελές τραπέζιο

Έτσι BK=QN=BC

άρα

μεσοκάθετος της

,άρα $\angle BCA= \angle QKB=2 \theta$ και

$5\theta =90^0$ άρα $\theta =18^0 \Rightarrow B=54^0,C=36^0$

: ίσες γωνίες,διπλάσια βάση.png (26.65 KiB) Προβλήθηκε 306 φορές

Μιχάλης Τσουρακάκης · #6

KARKAR έγραψε: ↑
Πέμ Δεκ 26, 2024 8:49 pm
Ίσες γωνίες , διπλάσια βάση.pngΤα σημεία της πλευράς του ορθογωνίου τριγώνου είναι τέτοια , ώστε τα τμήματα

να τριχοτομούν την γωνία $\hat{B}$ . Αν είναι : , μπορούμε άραγε να υπολογίσουμε την γωνία $\hat{B}$ ;

Αλλιώς

Είναι γνωστό ότι $\Phi =2cos36^0$

Με $SA=AN \Rightarrow SN=CT$ και προφανώς η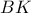

διχοτομεί την γωνία

, άρα

$\dfrac{CS}{SN} = \dfrac{BC}{BN}= \dfrac{BC}{BS}= \dfrac{CT}{ST} \Rightarrow \dfrac{CT+ST}{CT}= \dfrac{CT}{ST}$

Η τελευταία δίνει

$( \dfrac{CT}{ST})^2 - \dfrac{CT}{ST} -1=0 \Rightarrow \dfrac{CT}{ST}= \Phi = \dfrac{NS}{ST}= \dfrac{2AS}{ST} =2 \dfrac{AB}{BT}=2cos2 \theta$

Άρα $2cos36^0=2cos2 \theta \Rightarrow 2 \theta =36^0 \Rightarrow B=3 \theta =54^0$

: ίσες γωνίες,διπλάσια βάση1.png (34.19 KiB) Προβλήθηκε 297 φορές

Γιώργος Μήτσιος · #7

Καλημέρα σε όλους! Μια προσπάθεια και από μένα, εκφράζοντας τον θαυμασμό μου προς όλους τους συμμετέχοντες.
Δυστυχώς χωρίς σχήμα και μεγάλες δυσκολίες στην πληκτρολόγηση..

Φέρω $SEN \perp BT$ με $E\in BT, N \in BC$

Έστω γωνία B=3u

,

και χωρίς βλάβη TC=SN=2AS=2

Στο τρίγωνο SNC

έχουμε γωνίες S=2u, C=90^o-3u, N=90^o+u

.

Είναι ST=1/x

άρα

Ο νόμος ημιτόνων στο ίδιο τρίγωνο μας δίνει $\dfrac{2x}{2x+1}=\dfrac {cos3u} {cosu} =2(2cos^2 u-1)-1=2x-1$

Προκύπτει η εξίσωση 4x^2 - 2x-1=0

με δεκτή ρίζα $cos2u =x=\Phi/2$

συνεπώς 2u =36^0, B=54^o

Φιλικά, Γιώργος.

Ίσες γωνίες , διπλάσια βάση

Ίσες γωνίες , διπλάσια βάση

Re: Ίσες γωνίες , διπλάσια βάση

Re: Ίσες γωνίες , διπλάσια βάση

Re: Ίσες γωνίες , διπλάσια βάση

Re: Ίσες γωνίες , διπλάσια βάση

Re: Ίσες γωνίες , διπλάσια βάση

Re: Ίσες γωνίες , διπλάσια βάση

Μέλη σε σύνδεση