KARKAR έγραψε: ↑Τρί Ιαν 30, 2024 12:27 pm
Ταλαιπωρημένο τμήμα.pngΣημείο

κινείται στον ημιάξονα

. Η εφαπτομένη από το

προς τον κύκλο :

τέμνει τον

, στο σημείο

. Ονομάζω

την τομή της

με τον

και

την τομή της
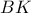
με τον

.
α) Υπολογίστε την ελάχιστη τιμή του μήκους του

. β) Εξετάστε αν υπάρχει μέγιστη τιμή του μήκους του

.

- Ταλαιπωρημένο τμή_ανάλυση.png (18.63 KiB) Προβλήθηκε 199 φορές
Θεωρώ το κύκλο,

και τέμνει την

στο

. Η γωνία

, ως εξωτερική του

συνεπώς η χορδή
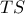
Γίνεται ελάχιστη όταν

. Το ίδιο συμπέρασμα συνάγεται αν το

είναι εσωτερικό του

.

- Ταλαιπωρημένο τμήμα_κατασκευή.png (15.6 KiB) Προβλήθηκε 199 φορές
Τώρα θα προκύψει το πιο πάνω σχήμα με το

, και τα ορθογώνια τρίγωνα

είναι και ισοσκελή .
Α; είναι

. Η ημιπερίμετρος του

είναι

.
Από τον τύπο του Ήρωνα και τον κλασικού που δίδει το εμβαδόν του έχω:


Τώρα από το Θ. διχοτόμου έχω :

και άρα λόγω της

,

και άρα :

β) Δεν έχω μέγιστη τιμή αλλά άνω φράγμα ίσο με

όταν η εφαπτομένη

τείνει να γίνει παράλληλη στον

.
 κινείται στον ημιάξονα
κινείται στον ημιάξονα  . Η εφαπτομένη από το
. Η εφαπτομένη από το  προς τον κύκλο :
προς τον κύκλο : 
 , στο σημείο
, στο σημείο  . Ονομάζω
. Ονομάζω  την τομή της
την τομή της  με τον
με τον  και
και  την τομή της
την τομή της 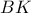 με τον
με τον  .
. . β) Εξετάστε αν υπάρχει μέγιστη τιμή του μήκους του
. β) Εξετάστε αν υπάρχει μέγιστη τιμή του μήκους του  .
.
 Επειδή ο εγγεγραμμένος κύκλος έχει ακτίνα
Επειδή ο εγγεγραμμένος κύκλος έχει ακτίνα 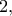 θα είναι
θα είναι  Έχουμε λοιπόν:
Έχουμε λοιπόν: 

 άρα το
άρα το  ελαχιστοποιείται όταν
ελαχιστοποιείται όταν  Επομένως,
Επομένως, 
 και τέμνει την
και τέμνει την  στο
στο  . Η γωνία
. Η γωνία  , ως εξωτερική του
, ως εξωτερική του  συνεπώς η χορδή
συνεπώς η χορδή 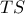
 . Το ίδιο συμπέρασμα συνάγεται αν το
. Το ίδιο συμπέρασμα συνάγεται αν το  , και τα ορθογώνια τρίγωνα
, και τα ορθογώνια τρίγωνα  είναι και ισοσκελή .
είναι και ισοσκελή . . Η ημιπερίμετρος του
. Η ημιπερίμετρος του  είναι
είναι  .
. 

 και άρα λόγω της
και άρα λόγω της  και άρα :
και άρα :
 όταν η εφαπτομένη
όταν η εφαπτομένη  τείνει να γίνει παράλληλη στον
τείνει να γίνει παράλληλη στον  και
και 
 Από τις παραπάνω σχέσεις και μετά τις πράξεις,
Από τις παραπάνω σχέσεις και μετά τις πράξεις,  Εύκολα διαπιστώνω ότι η συνάρτηση
Εύκολα διαπιστώνω ότι η συνάρτηση 
 Οπότε δεν έχουμε μέγιστη τιμή. Είναι όμως
Οπότε δεν έχουμε μέγιστη τιμή. Είναι όμως 