 είναι σταθερά , όπως και ο κύκλος
είναι σταθερά , όπως και ο κύκλος  . Από τα
. Από τα 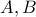 , διέρχεται μεταβλητός κύκλος ,
, διέρχεται μεταβλητός κύκλος , ο οποίος τέμνει τον
 στα σημεία
στα σημεία  . Δείξτε ότι το τμήμα
. Δείξτε ότι το τμήμα 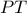 διέρχεται από σταθερό σημείο
διέρχεται από σταθερό σημείο  ,
,του τμήματος
 και με τα δεδομένα του σχήματος υπολογίστε το τμήμα
και με τα δεδομένα του σχήματος υπολογίστε το τμήμα  .
.Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 είναι σταθερά , όπως και ο κύκλος
είναι σταθερά , όπως και ο κύκλος  . Από τα
. Από τα 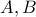 , διέρχεται μεταβλητός κύκλος ,
, διέρχεται μεταβλητός κύκλος ,  στα σημεία
στα σημεία  . Δείξτε ότι το τμήμα
. Δείξτε ότι το τμήμα 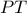 διέρχεται από σταθερό σημείο
διέρχεται από σταθερό σημείο  ,
, και με τα δεδομένα του σχήματος υπολογίστε το τμήμα
και με τα δεδομένα του σχήματος υπολογίστε το τμήμα  .
.. .
 η ακτίνα του δοθέντα κύκλου (εδώ
η ακτίνα του δοθέντα κύκλου (εδώ  ). To κέντρο
). To κέντρο  του κύκλου που διέρχεται από τα
του κύκλου που διέρχεται από τα  είναι στην μεσοκάθετο
είναι στην μεσοκάθετο  του
του  .
. ως προς τον δοθένα κύκλο είναι
ως προς τον δοθένα κύκλο είναι  . Του ίδιου σημείου η δύναμη ως προς τον κόκκινο κύκλο είναι
. Του ίδιου σημείου η δύναμη ως προς τον κόκκινο κύκλο είναι  . Άρα
. Άρα  , που σημαίνει
, που σημαίνει  σταθερό.
σταθερό.  βρίσκεται στην κάθετο του σταθερού
βρίσκεται στην κάθετο του σταθερού  και η κάθετος αυτή διέρχεται από σταθερό σημείο του
και η κάθετος αυτή διέρχεται από σταθερό σημείο του  (τόπος του Απολλωνίου για σταθερή διαφορά τετραγώνων). Αυτό ολοκληρώνει το ζητούμενο.
(τόπος του Απολλωνίου για σταθερή διαφορά τετραγώνων). Αυτό ολοκληρώνει το ζητούμενο.  είναι τώρα άμεσο για τα δοθέντα νούμερα (το αφήνω ως απλές πράξεις, άνευ ιδιαίτερης σημασίας).
είναι τώρα άμεσο για τα δοθέντα νούμερα (το αφήνω ως απλές πράξεις, άνευ ιδιαίτερης σημασίας). ( είναι η λύση του Μιχάλη ).
( είναι η λύση του Μιχάλη ). είναι τόσο άμεσος , θα ήθελα μια λύση ...
είναι τόσο άμεσος , θα ήθελα μια λύση ....
.Mihalis_Lambrou έγραψε: ↑Τρί Νοέμ 25, 2025 8:15 pmΤο μήκοςείναι τώρα άμεσο για τα δοθέντα νούμερα (το αφήνω ως απλές πράξεις, άνευ ιδιαίτερης σημασίας).
 . Η εύρεση του μήκους του
. Η εύρεση του μήκους του  χαλάει την κομψότητα και λιτότητα της άσκησης. Έχω τουλάχιστον τρεις τρόπους εύρεσης του μήκους αλλά η ενασχόληση με το θέμα είναι χωρίς ουσιαστική προσθήκη στις αρετές της άσκησης. Άλλωστε τα απαραίτητα Μαθηματικά είναι ήδη γραμμένα στα παραπάνω. Ας τα δούμε, κατά παρέκκλιση, γιατί θέλω να επισημάνω κάτι στο τέλος του παρόντος ποστ:
χαλάει την κομψότητα και λιτότητα της άσκησης. Έχω τουλάχιστον τρεις τρόπους εύρεσης του μήκους αλλά η ενασχόληση με το θέμα είναι χωρίς ουσιαστική προσθήκη στις αρετές της άσκησης. Άλλωστε τα απαραίτητα Μαθηματικά είναι ήδη γραμμένα στα παραπάνω. Ας τα δούμε, κατά παρέκκλιση, γιατί θέλω να επισημάνω κάτι στο τέλος του παρόντος ποστ: είναι στην ευθεία
είναι στην ευθεία  που έχει εξίσωση
που έχει εξίσωση  σημαίνει ότι
σημαίνει ότι  . Επίσης είναι
. Επίσης είναι 

 , δηλαδή
, δηλαδή  . Είναι τότε, από τις συντεταγμένες των
. Είναι τότε, από τις συντεταγμένες των  το μήκος
το μήκος 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης