 είναι εγγεγραμμένο σε κύκλο κέντρου
είναι εγγεγραμμένο σε κύκλο κέντρου  και έστω
και έστω  το μέσο της πλευράς
το μέσο της πλευράς  Ο κύκλος που
Ο κύκλος πουδιέρχεται από τα σημεία
 τέμνει την προέκταση της
τέμνει την προέκταση της 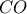 στο
στο 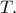 Αν η
Αν η  τέμνει την
τέμνει την  στο
στο 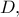 να
να δείξετε ότι
 είναι το ύψος του τριγώνου
είναι το ύψος του τριγώνου 
Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 είναι εγγεγραμμένο σε κύκλο κέντρου
είναι εγγεγραμμένο σε κύκλο κέντρου  και έστω
και έστω  το μέσο της πλευράς
το μέσο της πλευράς  Ο κύκλος που
Ο κύκλος που τέμνει την προέκταση της
τέμνει την προέκταση της 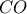 στο
στο 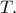 Αν η
Αν η  τέμνει την
τέμνει την  στο
στο 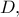 να
να  είναι το ύψος του τριγώνου
είναι το ύψος του τριγώνου 
Στο ισοσκελές τρίγωνοgeorge visvikis έγραψε: ↑Δευ Νοέμ 24, 2025 10:19 amΤο Ύψος..png
Τρίγωνοείναι εγγεγραμμένο σε κύκλο κέντρου
και έστω
το μέσο της πλευράς
Ο κύκλος που
διέρχεται από τα σημείατέμνει την προέκταση της
στο
Αν η
τέμνει την
στο
να
δείξετε ότιείναι το ύψος του τριγώνου



Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης