Περιορισμένος λόγος

KARKAR · #1

: Περιορισμένος λόγος.png (9.76 KiB) Προβλήθηκε 711 φορές

Το

είναι το έγκεντρο του ορθογωνίου τριγώνου ABC

. Ενδιαφερόμαστε για τον λόγο : $\lambda = \dfrac{(SBC)}{(ABC)}$ .

α) Ποια είναι η ελάχιστη τιμή του $\lambda$ ; .... β) Υπάρχει περίπτωση να είναι : $\lambda=\dfrac{1}{2}$ ;

γ) Βρείτε το "είδος" του τριγώνου για το οποίο είναι : $\lambda=\dfrac{13}{30}$ . Απαντήστε με όποια σειρά θέλετε .

#2

KARKAR έγραψε: ↑
Παρ Ιούλ 25, 2025 7:33 pm
Περιορισμένος λόγος.pngΤο είναι το έγκεντρο του ορθογωνίου τριγώνου . Ενδιαφερόμαστε για τον λόγο : $\lambda = \dfrac{(SBC)}{(ABC)}$ .

α) Ποια είναι η ελάχιστη τιμή του $\lambda$ ; .... β) Υπάρχει περίπτωση να είναι : $\lambda=\dfrac{1}{2}$ ;

γ) Βρείτε το "είδος" του τριγώνου για το οποίο είναι : $\lambda=\dfrac{13}{30}$ . Απαντήστε με όποια σειρά θέλετε .

Το

απέχει απόσταση

(ακτίνα εγγεγραμμένου) από κάθε πλευρά. Άρα

$\displaystyle{\dfrac{(SBC)}{(ABC)}=\dfrac {\frac {1}{2} ar }{\frac {1}{2} (a+b+c)r}=\dfrac {a}{a+b+c}}$

β) Από την τριγωνική ανισότητα έχουμε $\dfrac {a}{a+b+c}< \dfrac {a}{a+a}= \dfrac {1}{2}$ (ποτέ ίσο).

α) $\displaystyle{ \dfrac {a}{a+b+c}= \dfrac {a}{a+a \sin B+a \sin C}= \dfrac {1}{1+2 \sin \dfrac {B+C}{2} \cos \dfrac {B-C}{2}} = \dfrac {1}{1+2 \sin 45 \cos \dfrac {B-C}{2}} =$

$\displaystyle{=\dfrac {1}{1+\sqrt 2 \cos \dfrac {B-C}{2}}\ge \dfrac {1}{1+\sqrt 2}}}$ με ισότητα αν και μόνον αν B=C

(ισοσκελές).

γ) Ένα τέτοιο τρίγωνο είναι το a=13, b=12, c=5

και τα όμοιά του. To βλέπουμε με το μάτι αλλά αν λύναμε εξισώσεις, εδώ την $\displaystyle{\dfrac {a}{a+b+c}= \dfrac{13}{30}}$ , ισοδύναμα $\displaystyle{\dfrac {\sqrt {b^2+c^2}}{\sqrt {b^2+c^2}+b+c}= \dfrac{13}{30}}$ , οδηγούμαστε και πάλι στο τρίγωνο 5t, 12t, 13t

.

.

#3

Mihalis_Lambrou έγραψε: ↑
Παρ Ιούλ 25, 2025 10:14 pm

α) $\displaystyle{ \dfrac {a}{a+b+c}= \dfrac {a}{a+a \sin B+a \sin C}= \dfrac {1}{1+2 \sin \dfrac {B+C}{2} \cos \dfrac {B-C}{2}} =$

$\displaystyle{=\dfrac {1}{1+2 \sin 45 \cos \dfrac {B-C}{2}} = \dfrac {1}{1+\sqrt 2 \cos \dfrac {B-C}{2}}\ge \dfrac {1}{1+\sqrt 2}}}$ με ισότητα αν και μόνον αν (ισοσκελές).

Αλλιώς το α), για να αποφύγουμε την Τριγωνομετρία. Από την ανισότητα $2(b^2+c^2) \ge (b+c)^2$ (ισοδυναμεί με την $(b-c)^2\ge 0$ ) έχουμε

$\dfrac {a}{a+b+c}= \dfrac {\sqrt {b^2+c^2} }{\sqrt {b^2+c^2} +b+c }\ge \dfrac {\sqrt {b^2+c^2} }{\sqrt {b^2+c^2} +\sqrt {2} \sqrt {b^2+c^2}} = \dfrac {1}{1+\sqrt 2}}$

με ισότητα αν και μόνον αν b=c

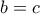(ισοσκελές)

Περιορισμένος λόγος

Περιορισμένος λόγος

Re: Περιορισμένος λόγος

Re: Περιορισμένος λόγος

Μέλη σε σύνδεση