 είναι το μέσο της βάσης
είναι το μέσο της βάσης  , τριγώνου
, τριγώνου  . Εντοπίστε σημεία
. Εντοπίστε σημεία 
των πλευρών
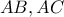 αντίστοιχα , τέτοια ώστε το τρίγωνο
αντίστοιχα , τέτοια ώστε το τρίγωνο 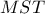 να είναι ισόπλευρο .
να είναι ισόπλευρο .Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 είναι το μέσο της βάσης
είναι το μέσο της βάσης  , τριγώνου
, τριγώνου  . Εντοπίστε σημεία
. Εντοπίστε σημεία 
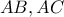 αντίστοιχα , τέτοια ώστε το τρίγωνο
αντίστοιχα , τέτοια ώστε το τρίγωνο 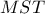 να είναι ισόπλευρο .
να είναι ισόπλευρο . και κορυφή
και κορυφή  .
. και κορυφή
και κορυφή  .
. και
και  .
.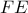 τέμνει την πλευρά
τέμνει την πλευρά  είναι το ζητούμενο σημείο
είναι το ζητούμενο σημείο  .
. , το τμήμα
, το τμήμα 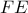 είναι ο γεωμετρικός τόπος του
είναι ο γεωμετρικός τόπος του  καθώς το
καθώς το  κινείται στην πλευρά
κινείται στην πλευρά  )
) επί της πλευράς
επί της πλευράς  ενός
ενός  παρακάτω εντοπίζονται σημεία
παρακάτω εντοπίζονται σημεία  και
και  επί των ευθειών
επί των ευθειών  και
και  αντίστοιχα που είναι τέτοια, ώστε το
αντίστοιχα που είναι τέτοια, ώστε το  να είναι ισόπλευρο.
να είναι ισόπλευρο. είναι η αρχή των αξόνων και ότι οι κορυφές του
είναι η αρχή των αξόνων και ότι οι κορυφές του  έχουν συντεταγμένες
έχουν συντεταγμένες  και
και 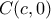 με
με  και
και 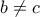
 και
και  ενώ όταν ορίζονται οι συντελεστές διεύθυνσης των ευθειών
ενώ όταν ορίζονται οι συντελεστές διεύθυνσης των ευθειών  και
και  με
με  και
και  αντίστοιχα.
αντίστοιχα. ως πλευρές ισόπλευρου.
ως πλευρές ισόπλευρου. μόνο αν
μόνο αν 
 μόνο αν
μόνο αν 
 τότε:
τότε: διότι το σημείο
διότι το σημείο  ανήκει στην ευθεία
ανήκει στην ευθεία 
 διότι το σημείο
διότι το σημείο  ανήκει στην ευθεία
ανήκει στην ευθεία 
![s^2 + \left[ P(s - b) \right]^2 = t^2 + \left[ Q(t - c) \right]^2 = (t - s)^2 + \left[ Q(t - c) - P(s - b) \right]^2 s^2 + \left[ P(s - b) \right]^2 = t^2 + \left[ Q(t - c) \right]^2 = (t - s)^2 + \left[ Q(t - c) - P(s - b) \right]^2](/forum/ext/geomar/texintegr/latexrender/pictures/c8b0eb7f511f2ab4220527aacaeec6fe.png)

 τότε
τότε 
 από τη θέση
από τη θέση  που τέμνει την ευθεία
που τέμνει την ευθεία  στο σημείο
στο σημείο  ενώ η μεσοκάθετη του
ενώ η μεσοκάθετη του  τέμνει την ευθεία
τέμνει την ευθεία  στο σημείο
στο σημείο 
 δεν χρειάζεται να είναι μέσο της
δεν χρειάζεται να είναι μέσο της 
Όλες είναι ωραίες. Αυτή όμως που μου έκανε μεγάλη εντύπωση είναι η πιο πάνω .duamba έγραψε: ↑Τρί Μάιος 20, 2025 7:36 pmΚαλησπέρα,
Μια κατασκευή άνευ τεκμηρίωσης (λόγω ελλιπούς χρόνου αλλά και κατανόησης).
paragwgi-isoplevrou.png
Κατασκευάζω ισόπλευρο τρίγωνο με πλευράκαι κορυφή
.
Επίσης κατασκευάζω ισόπλευρο με πλευράκαι κορυφή
.
Ενώνω τις κορυφέςκαι
.
Εκεί που ητέμνει την πλευρά
είναι το ζητούμενο σημείο
.
(Ξεκινώντας απο το τρίγωνο, το τμήμα
είναι ο γεωμετρικός τόπος του
καθώς το
κινείται στην πλευρά
)
Υποπτεύομαι ότι ως ωραίο πρόβλημα θα έχει λύση και με Απολλώνιο κύκλο.
 δεν είναι αναγκαστικά μέσο στο
δεν είναι αναγκαστικά μέσο στο  .
. για τον καλό λόγο και τον
για τον καλό λόγο και τον  για την ενθαρρυντική παρότρυνση.
για την ενθαρρυντική παρότρυνση. και
και  έχει επιτευχθεί η στροφή του τμήματος
έχει επιτευχθεί η στροφή του τμήματος  κατά 60 μοίρες θετικά γύρω απο το
κατά 60 μοίρες θετικά γύρω απο το  .
. απεικονίζω το σημείο
απεικονίζω το σημείο  του περιστραμμένου
του περιστραμμένου 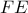 στο
στο  του
του  και άρα
και άρα  .
. έχω
έχω  εξ ου και το ζητούμενο.
εξ ου και το ζητούμενο.Ενδιαφέρουσα παραλλαγή, επιφυλάσσομαι να επανέλθω
 είναι τυχαίο ή το μέσο της
είναι τυχαίο ή το μέσο της  .
. φέρουμε ευθεία που να τέμνει την
φέρουμε ευθεία που να τέμνει την  στο
στο  και να σχηματίζει με την
και να σχηματίζει με την  γωνία
γωνία  μοιρών και από το
μοιρών και από το  ευθεία που να τέμνει την
ευθεία που να τέμνει την  στο
στο  και να σχηματίζει με την
και να σχηματίζει με την 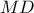 γωνία
γωνία  μοιρών. Γράφουμε το κύκλο
μοιρών. Γράφουμε το κύκλο  που επανατέμνει την
που επανατέμνει την  γενικά στο
γενικά στο  . To τρίγωνο
. To τρίγωνο 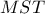 είναι ισόπλευρο γιατί έχει
είναι ισόπλευρο γιατί έχει  μοιρών και
μοιρών και  μοιρών.
μοιρών.Μία, επίσης, όμορφη κατασκευή και με εύκολη απόδειξη.ΝΙΚΟΣ έγραψε: ↑Δευ Μάιος 26, 2025 9:38 amΑξίζει τον κόπο.
Αν τοείναι τυχαίο ή το μέσο της
.
Από τοφέρουμε ευθεία που να τέμνει την
στο
και να σχηματίζει με την
γωνία
μοιρών και από το
ευθεία που να τέμνει την
στο
και να σχηματίζει με την
γωνία
μοιρών. Γράφουμε το κύκλο
που επανατέμνει την
γενικά στο
. To τρίγωνο
είναι ισόπλευρο γιατί έχει
μοιρών και
μοιρών.
Με αγάπη και εκτίμηση
Νίκος Κυριαζής
ΕΓΡΑΨΑΝ - ΕΙΠΑΝ
https://drive.google.com/file/d/1evwKsq ... lSCTw/view
Γιώργο σε ευχαριστώ πολύ.george visvikis έγραψε: ↑Δευ Μάιος 26, 2025 9:57 amΜία, επίσης, όμορφη κατασκευή και με εύκολη απόδειξη.ΝΙΚΟΣ έγραψε: ↑Δευ Μάιος 26, 2025 9:38 amΑξίζει τον κόπο.
Αν τοείναι τυχαίο ή το μέσο της
.
Από τοφέρουμε ευθεία που να τέμνει την
στο
και να σχηματίζει με την
γωνία
μοιρών και από το
ευθεία που να τέμνει την
στο
και να σχηματίζει με την
γωνία
μοιρών. Γράφουμε το κύκλο
που επανατέμνει την
γενικά στο
. To τρίγωνο
είναι ισόπλευρο γιατί έχει
μοιρών και
μοιρών.
Με αγάπη και εκτίμηση
Νίκος Κυριαζής
ΕΓΡΑΨΑΝ - ΕΙΠΑΝ
https://drive.google.com/file/d/1evwKsq ... lSCTw/view
Εκπληκτικής απλότητας και ομορφιάς κατασκευή και τεκμηρίωσηΝΙΚΟΣ έγραψε: ↑Δευ Μάιος 26, 2025 9:38 amΑξίζει τον κόπο.
Αν τοείναι τυχαίο ή το μέσο της
.
Από τοφέρουμε ευθεία που να τέμνει την
στο
και να σχηματίζει με την
γωνία
μοιρών και από το
ευθεία που να τέμνει την
στο
και να σχηματίζει με την
γωνία
μοιρών. Γράφουμε το κύκλο
που επανατέμνει την
γενικά στο
. To τρίγωνο
είναι ισόπλευρο γιατί έχει
μοιρών και
μοιρών.
Με αγάπη και εκτίμηση
Νίκος Κυριαζής
ΕΓΡΑΨΑΝ - ΕΙΠΑΝ
https://drive.google.com/file/d/1evwKsq ... lSCTw/view
 , αλλά εδώ είναι το κάτι άλλο .
, αλλά εδώ είναι το κάτι άλλο .Doloros έγραψε: ↑Δευ Μάιος 26, 2025 8:30 pmΕγγραφή ισοπλεύρου σε τρίγωνο_δια χειρός ΚΥΡΙΑΖΗ ΝΙΚΟΥ.pngΝΙΚΟΣ έγραψε: ↑Δευ Μάιος 26, 2025 9:38 amΑξίζει τον κόπο.
Αν τοείναι τυχαίο ή το μέσο της
.
Από τοφέρουμε ευθεία που να τέμνει την
στο
και να σχηματίζει με την
γωνία
μοιρών και από το
ευθεία που να τέμνει την
στο
και να σχηματίζει με την
γωνία
μοιρών. Γράφουμε το κύκλο
που επανατέμνει την
γενικά στο
. To τρίγωνο
είναι ισόπλευρο γιατί έχει
μοιρών και
μοιρών.
Με αγάπη και εκτίμηση
Νίκος Κυριαζής
ΕΓΡΑΨΑΝ - ΕΙΠΑΝ
https://drive.google.com/file/d/1evwKsq ... lSCTw/view
Εκπληκτικής απλότητας και ομορφιάς κατασκευή και τεκμηρίωση
Έχει πολλές ομοιότητες με τη λύση του, αλλά εδώ είναι το κάτι άλλο .
 είναι το σημείο τομής του περικύκλου
είναι το σημείο τομής του περικύκλου  με την
με την 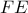 ) . Η λύση στηρίχθηκε στο "θεώρημα τριών ισοπλεύρων" , ( βλέπε εδώ )
) . Η λύση στηρίχθηκε στο "θεώρημα τριών ισοπλεύρων" , ( βλέπε εδώ )  ενός τριγώνου
ενός τριγώνου 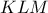 με δοθείσες γωνίες
με δοθείσες γωνίες  . Στα παραπάνω και οι τρεις είναι
. Στα παραπάνω και οι τρεις είναι  .
.  της
της  φέρνουμε ημιευθείες
φέρνουμε ημιευθείες  που σχηματίζουν γωνίες
που σχηματίζουν γωνίες  , όπως στο σχήμα. Φέρνουμε το
, όπως στο σχήμα. Φέρνουμε το  ώστε να σχηματίζει με την
ώστε να σχηματίζει με την 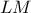 γωνία
γωνία  . Τότε από το εγγράψιμο
. Τότε από το εγγράψιμο  , το
, το 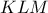 είναι το ζητούμενο. Απόδειξη τετριμμένη.
είναι το ζητούμενο. Απόδειξη τετριμμένη. με γωνίες ίσες προς τις δοθείσες
με γωνίες ίσες προς τις δοθείσες  , όπου
, όπου  πάνω στις πλευρές του
πάνω στις πλευρές του  . Φέρνουμε την
. Φέρνουμε την  η οποία τέμνει την
η οποία τέμνει την  στο
στο  . Φέρνουμε
. Φέρνουμε  και
και  . Από την ομοιότητα των
. Από την ομοιότητα των  έπεται ότι το
έπεται ότι το 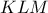 είναι το ζητούμενο. Τελειώσαμε.
είναι το ζητούμενο. Τελειώσαμε. το δοθέν. Κατασκευάζουμε τρίγωνο
το δοθέν. Κατασκευάζουμε τρίγωνο  με δοθείσες γωνίες
με δοθείσες γωνίες  . Τώρα περιγράφουμε στο
. Τώρα περιγράφουμε στο  τρίγωνο όμοιο με το δοθέν: Το πετυχαίνουμε γράφοντας ευθείες
τρίγωνο όμοιο με το δοθέν: Το πετυχαίνουμε γράφοντας ευθείες  που σχηματίζουν γωνία
που σχηματίζουν γωνία  και διέρχονται από τα
και διέρχονται από τα  . Κατόπιν φέρνουμε ευθεία
. Κατόπιν φέρνουμε ευθεία  που σχηματίζει με την
που σχηματίζει με την  γωνία
γωνία  και διέρχεται από
και διέρχεται από 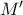 . Με άλλα λόγια έχουμε τρίγωνο
. Με άλλα λόγια έχουμε τρίγωνο  όμοιο με το δοθέν, το οποίο έχει μέσα του εγγεγραμμένο ένα τρίγωνο με δοθείσες γωνίες
όμοιο με το δοθέν, το οποίο έχει μέσα του εγγεγραμμένο ένα τρίγωνο με δοθείσες γωνίες  . Τώρα με ομοιότητα φέρνουμε το
. Τώρα με ομοιότητα φέρνουμε το  να έχει μέγεθος ίσο με το δοθέν. Τελειώσαμε.
να έχει μέγεθος ίσο με το δοθέν. Τελειώσαμε. .Mihalis_Lambrou έγραψε: ↑Πέμ Μάιος 29, 2025 8:45 amΑν θέλουμε, ακόμη, κάποια κορυφή να είναι συγκεκριμένο σημείο, οι παρακάτω κατασκευές χρειάζονται προσαρμογές. Θα επανέλθω, αν χρειαστεί, αλλά για την ώρα μένω στο πρόβλημα της εγγραφής (το οποίο είναι σαφώς πιο ενδιαφέρον και έχει άπειρες θέσεις που επιλύουν το πρόβλημα).
Μέθοδος 1. Από τυχαίοτης
φέρνουμε ημιευθείες
που σχηματίζουν γωνίες
, όπως στο σχήμα. Φέρνουμε το
ώστε να σχηματίζει με την
γωνία
. Τότε από το εγγράψιμο
, το
είναι το ζητούμενο. Απόδειξη τετριμμένη.
.
 σε τέτοια θέση ώστε η
σε τέτοια θέση ώστε η  να διέρχεται από το μέσον
να διέρχεται από το μέσον  της
της  (κατασκευή τετριμμένη). Τότε το
(κατασκευή τετριμμένη). Τότε το 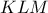 έχει τις ζητούμενες γωνίες και μία κορυφή του, η
έχει τις ζητούμενες γωνίες και μία κορυφή του, η  , είναι σε προκαθορισμένη θέση.
, είναι σε προκαθορισμένη θέση.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης