Λόγος και τμήμα

KARKAR · #1

: Λόγος και τμήμα.png (18.3 KiB) Προβλήθηκε 243 φορές

Με τα σημεία C , D

, τριχοτομούμε την ακτίνα OE=r

, ενός κύκλου . Η χορδή

είναι κάθετη στην

και διέρχεται από το

. Η

ξανατέμνει τον κύκλο στο

, ενώ οι προεκτάσεις των FA , OE

, τέμνονται

στο σημείο

. Υπολογίστε τον λόγο : $\dfrac{FA}{AS}$ , καθώς και το τμήμα

.

#2

KARKAR έγραψε: ↑
Τετ Απρ 09, 2025 9:00 am
Λόγος και τμήμα.pngΜε τα σημεία , τριχοτομούμε την ακτίνα , ενός κύκλου . Η χορδή είναι κάθετη στην

και διέρχεται από το . Η ξανατέμνει τον κύκλο στο , ενώ οι προεκτάσεις των , τέμνονται

στο σημείο . Υπολογίστε τον λόγο : $\dfrac{FA}{AS}$ , καθώς και το τμήμα .

: Λόγος και τμήμα.Κ.png (21.39 KiB) Προβλήθηκε 233 φορές

ΕΜΦΑΝΙΣΗ ΚΕΙΜΕΝΟΥ

#3

KARKAR έγραψε: ↑
Τετ Απρ 09, 2025 9:00 am
Λόγος και τμήμα.pngΜε τα σημεία , τριχοτομούμε την ακτίνα , ενός κύκλου . Η χορδή είναι κάθετη στην

και διέρχεται από το . Η ξανατέμνει τον κύκλο στο , ενώ οι προεκτάσεις των , τέμνονται

στο σημείο . Υπολογίστε τον λόγο : $\dfrac{FA}{AS}$ , καθώς και το τμήμα .

Με $r = 3k\,\,$ , επειδή η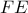

είναι διχοτόμος του $\vartriangle FCS$ και $ZF \bot FE$ η τετράδα : $\left( {C,S\backslash Z,E} \right)$ , αρμονική
.

: Λόγος και τμήμα ok.png (29.12 KiB) Προβλήθηκε 223 φορές

.

Από το λόγο , $\dfrac{{EC}}{{ES}} = \dfrac{{ZC}}{{ZS}} \Rightarrow \dfrac{{2k}}{x} = \dfrac{{4k}}{{6k + x}} \Rightarrow \boxed{x = 6k = 2r}$ . Επειδή το τετράπλευρο ACBE

είναι ρόμβος , $\boxed{\dfrac{{FA}}{{AS}} = \dfrac{{CE}}{{ES}} = \dfrac{{2k}}{{6k}} = \dfrac{1}{3}}$

#4

KARKAR έγραψε: ↑
Τετ Απρ 09, 2025 9:00 am
Λόγος και τμήμα.pngΜε τα σημεία , τριχοτομούμε την ακτίνα , ενός κύκλου . Η χορδή είναι κάθετη στην

και διέρχεται από το . Η ξανατέμνει τον κύκλο στο , ενώ οι προεκτάσεις των , τέμνονται

στο σημείο . Υπολογίστε τον λόγο : $\dfrac{FA}{AS}$ , καθώς και το τμήμα .

$\displaystyle A{Z^2} = ZD \cdot ZE = \frac{{5r}}{3}2r = \frac{{10{r^2}}}{3}$ και ομοίως $\displaystyle A{Z^2} = ZD \cdot ZE = \frac{{5r}}{3}2r = \frac{{10{r^2}}}{3},A{E^2} = \frac{{2{r^2}}}{3}.$

$\displaystyle \cos 2\theta = 2{\cos ^2}\theta - 1 = 2\frac{{A{Z^2}}}{{4{r^2}}} - 1 = \frac{2}{3}$ και $\displaystyle ZC = \frac{{4r}}{3} = 2r\frac{2}{3} = 2r\cos (A\widehat ZB)$ κι επειδή

είναι ύψος του τριγώνου AZB

το

θα είναι το ορθόκεντρο, άρα $BF\bot AZ.$

: Λόγος και τμήμα.Κ.png (21.39 KiB) Προβλήθηκε 207 φορές

To

είναι ισοσκελές τραπέζιο, οπότε AF=BE=AE=AC,

άρα η

είναι διχοτόμος της $F\widehat AC$ και

κατά συνέπεια η

διχοτόμος της $C\widehat AS,$ δηλαδή $\displaystyle \frac{{FA}}{{AS}} = \frac{{AC}}{{AS}} = \frac{{CE}}{{ES}} = \frac{{ZC}}{{ZS}} \Leftrightarrow \frac{{2r}}{x} = \frac{{4r}}{{2r + x}}$

Άρα, $\boxed{x=2r}$ και $\boxed{\frac{FA}{AS}=\frac{1}{3}}$

Μιχάλης Τσουρακάκης · #5

KARKAR έγραψε: ↑
Τετ Απρ 09, 2025 9:00 am
Λόγος και τμήμα.pngΜε τα σημεία , τριχοτομούμε την ακτίνα , ενός κύκλου . Η χορδή είναι κάθετη στην

και διέρχεται από το . Η ξανατέμνει τον κύκλο στο , ενώ οι προεκτάσεις των , τέμνονται

στο σημείο . Υπολογίστε τον λόγο : $\dfrac{FA}{AS}$ , καθώς και το τμήμα .

Προφανώς το

είναι κ.βάρους του τριγώνου FEZ

,άρα

κι έστω $ZE \cap FS=N$

Επειδή AEBC

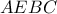είναι ρόμβος,θα είναι $\angle FBA= \angle EBA$ άρα τα τόξα FA,AE

είναι

ίσα,συνεπώς η

είναι διχοτόμος της γωνίας FZN

επομένως μεσοκάθετη της

,άρα

Επίσης η

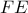διχοτομεί την $\angle BFA$ άρα είναι μεσοκάθετη της

,επομένως $NE=EM=MZ= \dfrac{2r}{3}$ .Είναι

$OA//EN \Rightarrow \dfrac{SE}{SO}= \dfrac{NE}{OA} = \dfrac{ \dfrac{2r}{3} }{r}= \dfrac{2}{3}$ κι επειδή

μέσον της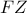

το

είναι κ.βάρους του τριγώνου FZS

Άρα

και $\dfrac{FA}{FS} = \dfrac{1}{3}$

: Λόγος και τμήμα.png (37.35 KiB) Προβλήθηκε 170 φορές

Λόγος και τμήμα

Λόγος και τμήμα

Re: Λόγος και τμήμα

Re: Λόγος και τμήμα

Re: Λόγος και τμήμα

Re: Λόγος και τμήμα

Μέλη σε σύνδεση