 του τριγώνου
του τριγώνου  , τέμνει τον περίκυκλό του στο σημείο
, τέμνει τον περίκυκλό του στο σημείο  .
.Έστω
 σημείο του μικρού τόξου
σημείο του μικρού τόξου  . Η
. Η 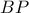 τέμνει την
τέμνει την  στο
στο  , ενώ οι προεκτάσεις
, ενώ οι προεκτάσεις των
 , τέμνονται στο
, τέμνονται στο 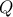 . Δείξτε ότι τα σημεία :
. Δείξτε ότι τα σημεία :  , είναι ομοκυκλικά .
, είναι ομοκυκλικά .Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 του τριγώνου
του τριγώνου  , τέμνει τον περίκυκλό του στο σημείο
, τέμνει τον περίκυκλό του στο σημείο  .
. σημείο του μικρού τόξου
σημείο του μικρού τόξου  . Η
. Η 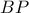 τέμνει την
τέμνει την  στο
στο  , ενώ οι προεκτάσεις
, ενώ οι προεκτάσεις  , τέμνονται στο
, τέμνονται στο 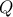 . Δείξτε ότι τα σημεία :
. Δείξτε ότι τα σημεία :  , είναι ομοκυκλικά .
, είναι ομοκυκλικά . . Let
. Let  be a convex pentagon having a circumcircle and satisfying
be a convex pentagon having a circumcircle and satisfying  . The
. The is the intersection of the diagonals
is the intersection of the diagonals  and
and  . The lines
. The lines 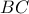 and
and intersect in point
intersect in point 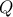 .
. is parallel to the diagonal
is parallel to the diagonal 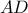 . (Gottfried Perz)
. (Gottfried Perz) is isosceles, which implies that the tangent to circle in
is isosceles, which implies that the tangent to circle in  is parallel to
is parallel to 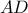 .
. : The intersection point of the
: The intersection point of the and
and  is
is , the intersection point of the opposite sides
, the intersection point of the opposite sides  and
and  is
is 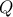 ,
, and
and  is the point at infinity corresponding
is the point at infinity corresponding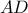 . Therefore,
. Therefore, is parallel to
is parallel to 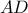 . (Stefan Leopoldseder) Αυστρία
. (Stefan Leopoldseder) Αυστρία  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες