george visvikis έγραψε:Σημείο

κινείται σε ημικύκλιο κέντρου

και διαμέτρου

Αν

είναι η προβολή του

στη διάμετρο και

το μέσο του

α) να εντοπίσετε τη θέση του

ώστε το τετράπλευρο

να είναι αμφιγράψιμο.
β) Αν

είναι οι εγγεγραμμένοι κύκλοι του τετραπλεύρου

και του τριγώνου

αντίστοιχα,
να δείξετε ότι


Για ευκολία στις πράξεις θεωρήστε ότι

Χρησιμοποιώ το σχήμα της εκφώνησης.

Έστω ότι έχει βρεθεί το σημείο

ώστε το εγγράψιμο πάντοτε τετράπλευρο

να είναι και περιγράψιμο.
Από

και

προκύπτει ότι το

έχει άξονα συμμετρίας την ευθεία της διαμέτρου

του περικύκλου του και επομένως έχουμε

και

Από

και

λόγω


Από

προκύπτει εύκολα η κατασκευή του σημείου

ως εξής:
Έστω

το σημείο στο εσωτερικό του δοσμένου ημικυκλίου

, ώστε να είναι

και

.
Η ευθεία

τέμνει το ημικύκλιο

στο σημείο έστω

και ισχύει

λόγω ομοιοθεσίας,
όπου

και

Ομοίως ( δεύτερη λύση ), η ευθεία

τέμνει το ημικύκλιο

στο σημείο έστω

και ισχύει

όπου

και

και το

ζητούμενο έχει λυθεί.

Από τα όμοια ορθογώνια τρίγωνα

έχουμε:



Από το ορθογώνιο τρίγωνο

έχουμε


Από την ομοιότητα των

έχουμε επίσης

( από ίσους λόγους ομόλογων τμημάτων σε όμοια τρίγωνα ).
Από
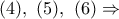


και το

ζητούμενο έχει αποδειχθεί.
Κώστας Βήττας.
ΥΓ. Από τα όμοια ορθογώνια τρίγωνα

προκύπτει

και επομένως το σημείο

( ομοίως και το

), είναι κορυφή του κανονικού ημιεξαγώνου που εγγράφεται στο δοσμένο ημικύκλιο

 κινείται σε ημικύκλιο κέντρου
κινείται σε ημικύκλιο κέντρου  και διαμέτρου
και διαμέτρου  Αν
Αν  είναι η προβολή του
είναι η προβολή του  στη διάμετρο
στη διάμετρο  το μέσο του
το μέσο του  α) να εντοπίσετε τη θέση του
α) να εντοπίσετε τη θέση του  ώστε το τετράπλευρο
ώστε το τετράπλευρο  να είναι αμφιγράψιμο.
να είναι αμφιγράψιμο. είναι οι εγγεγραμμένοι κύκλοι του τετραπλεύρου
είναι οι εγγεγραμμένοι κύκλοι του τετραπλεύρου  και του τριγώνου
και του τριγώνου 

 Για ευκολία στις πράξεις θεωρήστε ότι
Για ευκολία στις πράξεις θεωρήστε ότι 

 Έστω ότι έχει βρεθεί το σημείο
Έστω ότι έχει βρεθεί το σημείο  ώστε το εγγράψιμο πάντοτε τετράπλευρο
ώστε το εγγράψιμο πάντοτε τετράπλευρο  και
και  προκύπτει ότι το
προκύπτει ότι το  του περικύκλου του και επομένως έχουμε
του περικύκλου του και επομένως έχουμε  και
και 
 και
και  λόγω
λόγω 

 προκύπτει εύκολα η κατασκευή του σημείου
προκύπτει εύκολα η κατασκευή του σημείου  το σημείο στο εσωτερικό του δοσμένου ημικυκλίου
το σημείο στο εσωτερικό του δοσμένου ημικυκλίου  , ώστε να είναι
, ώστε να είναι  και
και  .
. τέμνει το ημικύκλιο
τέμνει το ημικύκλιο  λόγω ομοιοθεσίας,
λόγω ομοιοθεσίας,  και
και 
 τέμνει το ημικύκλιο
τέμνει το ημικύκλιο  και ισχύει
και ισχύει 
 και
και  και το
και το  ζητούμενο έχει λυθεί.
ζητούμενο έχει λυθεί.  έχουμε:
έχουμε:


 έχουμε
έχουμε 

 ( από ίσους λόγους ομόλογων τμημάτων σε όμοια τρίγωνα ).
( από ίσους λόγους ομόλογων τμημάτων σε όμοια τρίγωνα ).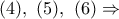

 και το
και το  ζητούμενο έχει αποδειχθεί.
ζητούμενο έχει αποδειχθεί. προκύπτει
προκύπτει  και επομένως το σημείο
και επομένως το σημείο  ), είναι κορυφή του κανονικού ημιεξαγώνου που εγγράφεται στο δοσμένο ημικύκλιο
), είναι κορυφή του κανονικού ημιεξαγώνου που εγγράφεται στο δοσμένο ημικύκλιο 