 , η κορυφή
, η κορυφή  , βρίσκεται πάνω στην μεσοκάθετη
, βρίσκεται πάνω στην μεσοκάθετητης πλευράς
 . Βρείτε το ελάχιστο άνω και το μέγιστο κάτω φράγμα , για τον λόγο :
. Βρείτε το ελάχιστο άνω και το μέγιστο κάτω φράγμα , για τον λόγο : 
Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 , η κορυφή
, η κορυφή  , βρίσκεται πάνω στην μεσοκάθετη
, βρίσκεται πάνω στην μεσοκάθετη . Βρείτε το ελάχιστο άνω και το μέγιστο κάτω φράγμα , για τον λόγο :
. Βρείτε το ελάχιστο άνω και το μέγιστο κάτω φράγμα , για τον λόγο : 
 , με τον λόγο
, με τον λόγο  ,
,Ας είναι μοναδιαίες οι πλευρές του ισόπλευρου πενταγώνου
 και ας είναι
και ας είναι  και
και  οπότε βεβαίως
οπότε βεβαίως  και, από Νόμο Συνημιτόνων στο
και, από Νόμο Συνημιτόνων στο 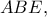
 Ισχύει όμως -- βλέπε συνημμένο -- και η
Ισχύει όμως -- βλέπε συνημμένο -- και η  οπότε λαμβάνουμε την βασική ισότητα γωνιών
οπότε λαμβάνουμε την βασική ισότητα γωνιών
 ως συνάρτηση της γωνίας
ως συνάρτηση της γωνίας 

 όσο αυξάνεται η γωνία
όσο αυξάνεται η γωνία 

 καθώς η γωνία
καθώς η γωνία  πράγματι μεταβάλλεται από την
πράγματι μεταβάλλεται από την  όπου
όπου  (ισοσκελές τρίγωνο), ως την
(ισοσκελές τρίγωνο), ως την  όπου
όπου  (ισοσκελές τραπέζιο).
(ισοσκελές τραπέζιο).  και
και  δίνουν άμεσα τα ζητούμενα φράγματα, καθώς από Νόμο Συνημιτόνων στα τρίγωνα
δίνουν άμεσα τα ζητούμενα φράγματα, καθώς από Νόμο Συνημιτόνων στα τρίγωνα  και
και  προκύπτει άμεσα η
προκύπτει άμεσα η  ... και όσο ο παρονομαστής αυξάνεται ο αριθμητής μειώνεται (σύμφωνα και με τα παραπάνω), κλπ
... και όσο ο παρονομαστής αυξάνεται ο αριθμητής μειώνεται (σύμφωνα και με τα παραπάνω), κλπ ως συνάρτησης της γωνίας
ως συνάρτησης της γωνίας  ... έχοντας προσθέσει και το απαραίτητο
... έχοντας προσθέσει και το απαραίτητο  στον τύπο της
στον τύπο της 
Μέλη σε αυτήν τη Δ. Συζήτηση: Bing [Bot] και 1 επισκέπτης