 και
και  ενός κύκλου
ενός κύκλου  είναι κάθετες . Στην εφαπτομένη του κύκλου στο
είναι κάθετες . Στην εφαπτομένη του κύκλου στο 
θεωρούμε σημείο
 , φέρουμε την
, φέρουμε την  - η οποία τέμνει τον κύκλο στο
- η οποία τέμνει τον κύκλο στο  - και ονομάζουμε
- και ονομάζουμε 
το μέσο της χορδής
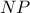 . Πώς πρέπει να επιλέξουμε το
. Πώς πρέπει να επιλέξουμε το  , ώστε η
, ώστε η  να διέλθει από το
να διέλθει από το  ;
;Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 και
και  ενός κύκλου
ενός κύκλου  είναι κάθετες . Στην εφαπτομένη του κύκλου στο
είναι κάθετες . Στην εφαπτομένη του κύκλου στο 
 , φέρουμε την
, φέρουμε την  - η οποία τέμνει τον κύκλο στο
- η οποία τέμνει τον κύκλο στο  - και ονομάζουμε
- και ονομάζουμε 
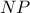 . Πώς πρέπει να επιλέξουμε το
. Πώς πρέπει να επιλέξουμε το  , ώστε η
, ώστε η  να διέλθει από το
να διέλθει από το  ;
;.
 . Έχουμε
. Έχουμε  και
και  , όπου
, όπου  το ζητούμενο.
το ζητούμενο.  είναι η
είναι η  , οπότε το
, οπότε το  είναι η τομή αυτής και του κύκλου
είναι η τομή αυτής και του κύκλου 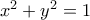 . Βγαίνει
. Βγαίνει  (άμεσο).
(άμεσο). της
της 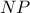 είναι το
είναι το  .
.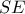 , δηλαδή την
, δηλαδή την  . Θέτοντας τις συντεταγμένες του
. Θέτοντας τις συντεταγμένες του  στην τελευταία μας ανάγει στην εξίσωση
στην τελευταία μας ανάγει στην εξίσωση  , και άρα στην
, και άρα στην 

 δεν κατασκευάζεται. Ίσως κάνω λάθος, αλλά το Θεώρημα Wantzel δίνει αμέσως την απάντηση (δεν το ελέγχω).
δεν κατασκευάζεται. Ίσως κάνω λάθος, αλλά το Θεώρημα Wantzel δίνει αμέσως την απάντηση (δεν το ελέγχω). του
του  Επειδή
Επειδή  άρα
άρα  Όμως
Όμως  άρα από το θεώρημα κεντρικής δέσμης το
άρα από το θεώρημα κεντρικής δέσμης το  είναι το μέσο του
είναι το μέσο του  Επειδή
Επειδή  έπεται
έπεται  Θέτοντας τώρα
Θέτοντας τώρα  είναι
είναι 


![\displaystyle \boxed{\cos \theta= \sqrt[3]{\frac{17}{27}+\sqrt{\frac{11}{27}}}+\sqrt[3]{\frac{17}{27}-\sqrt{\frac{11}{27}}}-\frac{1}{3}}. \displaystyle \boxed{\cos \theta= \sqrt[3]{\frac{17}{27}+\sqrt{\frac{11}{27}}}+\sqrt[3]{\frac{17}{27}-\sqrt{\frac{11}{27}}}-\frac{1}{3}}.](/forum/ext/geomar/texintegr/latexrender/pictures/f215b151e3847f200a5bc733501627b4.png)
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες