konargyr14 έγραψε: ↑Τετ Απρ 16, 2025 4:58 pm
Καλησπέρα. Μια λύση για το (α).
Το σημείο

ανήκει στην πολική του

προς τον κύκλο

, άρα από το θεώρημα La Hire η πολική του

προς τον ίδιο κύκλο θα περνά από το

. Συνεπώς η

είναι η πολική του

προς τον κύκλο

, αφού το
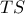
είναι εφαπτόμενο τμήμα στον

Αν

η τομή της

, με την χορδή

, τότε η τετράδα των σημείων

είναι αρμονική (αφού η

είναι η πολική του

). Στο πλήρες τετράπλευρο

τώρα, οι διαγώνιοι

τέμνονται στο

και άρα η τρίτη διαγώνιος

θα τέμνει την

στο συζηγές αρμονικό του

, δηλαδή το

. Συνεπώς οι ευθείες

συντρέχουν στο

και άρα τα σημεία

είναι συνευθειακά.
Κωνσταντίνος
Προσθέτω τη λύση για το δεύτερο ερώτημα (και το σχήμα):

και άρα

οπότε το

είναι ισόπλευρο (αφού

) και

Θέτουμε για ευκολία

. Από θεώρημα Μενελάου στο τρίγωνο

με διατέμνουσα την

παίρνουμε:

Από θεώρημα Μενελάου στο τρίγωνο

με διατέμνουσα την

παίρνουμε:

Από θεώρημα Μενελάου στο τρίγωνο

με διατέμνουσα την

παίρνουμε:

Η παράλληλη από το

προς το

τέμνει το

στο

. Τότε

άρα

και

(αφού

λόγω γωνίας χορδής και εφαπτομένης)
Συνεπώς τα

είναι εγγράψιμμα και άρα το

είναι εγγράψιμμο, οπότε

, οπότε

και

.
Άρα το

είναι παραλληλόγραμμο και έτσι έχουμε:

και

. Αντικαθιστώντας στην πρώτη από αυτές

, παίρνουμε:

Οπότε τελικά

Κωνσταντίνος

- 1.png (127.27 KiB) Προβλήθηκε 135 φορές
τελευταία επεξεργασία από
konargyr14 σε Κυρ Απρ 20, 2025 1:15 pm, έχει επεξεργασθεί 1 φορά συνολικά.
 , εξωτερικό του κύκλου
, εξωτερικό του κύκλου  , φέρουμε τα εφαπτόμενα τμήματα :
, φέρουμε τα εφαπτόμενα τμήματα :  . Από σημείο
. Από σημείο  της προέκτασης
της προέκτασης  , φέρουμε το εφαπτόμενο τμήμα
, φέρουμε το εφαπτόμενο τμήμα  . Οι
. Οι  τέμνουν τις
τέμνουν τις  , στα σημεία
, στα σημεία  αντίστοιχα .
αντίστοιχα .  είναι συνευθειακά . β) Αν :
είναι συνευθειακά . β) Αν :  , υπολογίστε το
, υπολογίστε το  , ώστε :
, ώστε :  .
.
 είναι η πολική του
είναι η πολική του  , αφού το
, αφού το 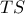 είναι εφαπτόμενο τμήμα στον
είναι εφαπτόμενο τμήμα στον  Αν
Αν  η τομή της
η τομή της  είναι αρμονική (αφού η
είναι αρμονική (αφού η  τώρα, οι διαγώνιοι
τώρα, οι διαγώνιοι  τέμνονται στο
τέμνονται στο  θα τέμνει την
θα τέμνει την  συντρέχουν στο
συντρέχουν στο  είναι συνευθειακά.
είναι συνευθειακά.
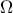 είναι η χορδή των επαφών
είναι η χορδή των επαφών  με το τετράπλευρο
με το τετράπλευρο  να είναι αρμονικό .
να είναι αρμονικό . , της ευθείας
, της ευθείας  θα περνά από τα σημεία
θα περνά από τα σημεία  και
και  στο
στο  με την τετράδα ,
με την τετράδα ,  αρμονική οπότε αναγκαστικά
αρμονική οπότε αναγκαστικά  .
. ισόπλευρο πλευράς
ισόπλευρο πλευράς  . Επίσης
. Επίσης 
 με διατέμνουσα
με διατέμνουσα  κι έχω :
κι έχω :  (1)
(1) κι έχω :
κι έχω :  (2)
(2)
 σύμφωνα με τα σημεία
σύμφωνα με τα σημεία 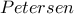 ( Α. Δημητρίου Θέμα 16)
( Α. Δημητρίου Θέμα 16) . Αν
. Αν  από Θ. συνημίτονου στο
από Θ. συνημίτονου στο 
 οπότε
οπότε  .
. έχω:
έχω:  και από τις
και από τις  προκύπτει ,
προκύπτει ,  . Από το Θ. συνημίτονου στο
. Από το Θ. συνημίτονου στο  έχω
έχω  Από τις
Από τις  διώχνω είτε το
διώχνω είτε το  και βρίσκω το
και βρίσκω το  ,είτε το
,είτε το  , Με διώξιμο του
, Με διώξιμο του  και έτσι :
και έτσι :  .
. και άρα
και άρα 
 είναι ισόπλευρο (αφού
είναι ισόπλευρο (αφού  ) και
) και
 . Από θεώρημα Μενελάου στο τρίγωνο
. Από θεώρημα Μενελάου στο τρίγωνο  με διατέμνουσα την
με διατέμνουσα την  παίρνουμε:
παίρνουμε:
 με διατέμνουσα την
με διατέμνουσα την  παίρνουμε:
παίρνουμε:
 παίρνουμε:
παίρνουμε:
 προς το
προς το  τέμνει το
τέμνει το  . Τότε
. Τότε  άρα
άρα  και
και  (αφού
(αφού  λόγω γωνίας χορδής και εφαπτομένης)
λόγω γωνίας χορδής και εφαπτομένης) είναι εγγράψιμμα και άρα το
είναι εγγράψιμμα και άρα το  είναι εγγράψιμμο, οπότε
είναι εγγράψιμμο, οπότε  , οπότε
, οπότε  και
και  .
. είναι παραλληλόγραμμο και έτσι έχουμε:
είναι παραλληλόγραμμο και έτσι έχουμε: και
και  . Αντικαθιστώντας στην πρώτη από αυτές
. Αντικαθιστώντας στην πρώτη από αυτές  , παίρνουμε:
, παίρνουμε:
