KARKAR έγραψε: ↑Δευ Ιουν 19, 2023 9:09 am
Σταθερός λόγος.pngΤο σημείο

κινείται στην διχοτόμο

του τριγώνου

. Η

τέμνει την

στο σημείο

, ενώ
οι

τέμνονται στο

. Δείξτε ότι ο γεωμετρικός τόπος του

είναι το τμήμα
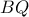
και υπολογίστε
τον λόγο

, αν το τρίγωνο

είναι ορθογώνιο , με κάθετες πλευρές :
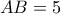
και :

.

- Σταθερός λόγος_1.png (8.85 KiB) Προβλήθηκε 447 φορές
Η πολική του

ως προς τις ευθείες

είναι η ευθεία που συνδέει το

με το

για οποιαδήποτε θέση του

επί της σταθερής διχοτόμου

.
Αν αυτή η ευθεία τμήση την

στο

, η δέσμη

είναι αρμονική καθώς και η τετράδα

.
Αφού τα σημεία

είναι σταθερά θα είναι σταθερό και το

γιατί ισχύει :

, σχέση που μας εξασφαλίζει ότι το

διατρέχει το σταθερό
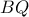
.

- Σταθερός λόγος_2.png (11.16 KiB) Προβλήθηκε 447 φορές
Αν τώρα το

είναι ορθογώνιο στο

και

θα είναι

.
Από το Θ. εσωτ. διχοτόμου ,

και ομοίως

Θέτω

και από την αρμονική αναλογία ,

συνεπώς:

.
 κινείται στην διχοτόμο
κινείται στην διχοτόμο  του τριγώνου
του τριγώνου  . Η
. Η  τέμνει την
τέμνει την  στο σημείο
στο σημείο  , ενώ
, ενώ τέμνονται στο
τέμνονται στο  . Δείξτε ότι ο γεωμετρικός τόπος του
. Δείξτε ότι ο γεωμετρικός τόπος του  είναι το τμήμα
είναι το τμήμα 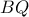 και υπολογίστε
και υπολογίστε , αν το τρίγωνο
, αν το τρίγωνο  είναι ορθογώνιο , με κάθετες πλευρές :
είναι ορθογώνιο , με κάθετες πλευρές : 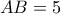 και :
και :  .
.
 ως προς τις ευθείες
ως προς τις ευθείες  που είναι η
που είναι η 
 με το
με το  στο
στο  , η δέσμη
, η δέσμη  είναι αρμονική καθώς και η τετράδα
είναι αρμονική καθώς και η τετράδα  .
. είναι σταθερά θα είναι σταθερό και το
είναι σταθερά θα είναι σταθερό και το  , σχέση που μας εξασφαλίζει ότι το
, σχέση που μας εξασφαλίζει ότι το  είναι ορθογώνιο στο
είναι ορθογώνιο στο  θα είναι
θα είναι  .
. και ομοίως
και ομοίως 
 και από την αρμονική αναλογία ,
και από την αρμονική αναλογία ,  συνεπώς:
συνεπώς: