Σημεία παραβολής

KARKAR · #1

: Σημεία παραβολής.png (8.96 KiB) Προβλήθηκε 468 φορές

Το $k \in \mathbb{R}$ είναι σταθερός μη μηδενικός αριθμός . Δείξτε ότι η παραβολή : y=x^2+ax+ka

, για κάθε τιμή του $a \in \mathbb{R}$

διέρχεται από σταθερό σημείο , το οποίο να βρείτε στην περίπτωση που : a=k

και η παραβολή διέρχεται και από το (1,7)

.

#2

KARKAR έγραψε: ↑
Πέμ Δεκ 22, 2022 1:45 pm
Σημεία παραβολής.pngΤο $k \in \mathbb{R}$ είναι σταθερός μη μηδενικός αριθμός . Δείξτε ότι η παραβολή : , για κάθε τιμή του $a \in \mathbb{R}$

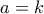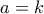διέρχεται από σταθερό σημείο , το οποίο να βρείτε στην περίπτωση που : και η παραβολή διέρχεται και από το .

Όλες οι εν λόγω παραβολές διέρχονται από το σημείο $(-k,\, k^2)$ . Ο έλεχγος άμεσος. Πώς το βρήκα; Έβαλα

εκείνη την τιμή που μηδενίζει το τμήμα της συνάρτησης που έχει

, δηλαδή το ax+ak

. Aυτό εξαφανίζεται βέβαια αν 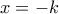x=-k

. Αυτό μου προδίδει το σταθερό σημείο, που είναι εκείνο που έγραψα.

Αν a=k

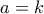, η συνάρηση γίνεται y=x^2+kx+k^2

. Aν διέρχεται από το $(1,\, 7)$ , έχουμε 7=1^2+k+k^2

. Άρα

ή

, που επαληθεύουν.

Σημεία παραβολής

Σημεία παραβολής

Re: Σημεία παραβολής

Μέλη σε σύνδεση