 διαιρέσαμε την διάμετρο
διαιρέσαμε την διάμετρο  ενός ημικυκλίου , σε δύο ακέραια τμήματα
ενός ημικυκλίου , σε δύο ακέραια τμήματα  ,
, και φέραμε το κάθετο στην διάμετρο , τμήμα
και φέραμε το κάθετο στην διάμετρο , τμήμα  , επί του οποίου θεωρήσαμε σημείο
, επί του οποίου θεωρήσαμε σημείο  ,
,τέτοιο ώστε :
 , με
, με  . Η
. Η  ξανατέμνει το τόξο στο σημείο
ξανατέμνει το τόξο στο σημείο  .
.Βρείτε το γινόμενο
 , για
, για  και εξηγήστε γιατί είναι πάντα ακέραιο .
και εξηγήστε γιατί είναι πάντα ακέραιο .
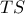 μέχρι το
μέχρι το  . Είναι τότε
. Είναι τότε  (άμεσο). Από το ορθογώνιο τρίγωνο
(άμεσο). Από το ορθογώνιο τρίγωνο  είναι
είναι  . Άρα από την δύναμη του σημείου
. Άρα από την δύναμη του σημείου  , έχουμε
, έχουμε  ακέραιος για όλα τα ακέραια
ακέραιος για όλα τα ακέραια  , που είναι το αποδεικτέο.
, που είναι το αποδεικτέο.