
Με την ευκαιρία θα σου δώσω ξανά την συμβουλή που έδωσα στο ποστ #6
εδώ
Κοιτώντας την φορμαλιστική λύση που έδωσες, κάνεις άλλη μία φορά τα εύκολα, δύσκολα. Στα Μαθηματικά πρέπει να ακολουθούμε τον δρόμο της απλότητας και κομψότητας. Στην συγκεκριμένη περίπτωση, η άσκηση είναι αρκετά απλή και λύνεται σε λίγες γραμμές μόνο με εφόδια του Δημοτικού. Το να εξετάζεις συνάρτηση από το

στο δυναμοσύνολό του με την ιδιότητα
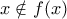
(για να δηλώσεις το αυτονόητο ότι κανείς δεν έπαιξε παρτίδα με τον εαυτό του) και
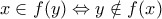
(για να δηλώσεις το αυτονόητο ότι αν ο

έπαιξε παρτίδα με τον

τότε και

έπαιξε με τον

) ξεπερνά το μέτρο.
Στα Μαθηματικά χρησιμοποιούμε τα σύμβολα όταν βοηθούν και διευκολύνουν τον συλλογισμό. Το να χρησιμοποιούμε τα σύμβολα στην ανάποδη κατεύθυνση, δηλαδή να συσκοτίσουμε τον συλλογισμό μπερδεύοντας τον αναγνώστη σε νοητικές ακροβασίες είναι πρακτική προς αποφυγήν. Θυμίζει τους Αλχημιστές του Μεσαίωνα και της Αναγέννησης που προσποιούνταν συστηματικά ότι έγραφαν σπουδαία πράγματα τα οποία ήσαν κατανοητά μόνο στους μεμυημένους, όταν στην πραγματικότητα έγραφαν ταυτολογίες ή ανυπαρκτολογίες.
Αν διδάσκεις τους μαθητές σου με αυτό το ύφος, θα τους χάσεις όλους. Σου συνιστώ, λοιπόν, όταν γράφεις για απλά πράγματα, το στυλ γραφής πρέπει να είναι αναλόγως απλό. Να μην φαίνεται περισπούδαστο και βαθύ όταν δεν είναι.
 νάνοι, που τα ονόματά τους είναι Α, Β, Γ, Δ, Ε, Ζ και Η, έπαιξαν μεταξύ τους μερικές παρτίδες σκάκι. Ο καθένας έπαιξε το πολύ μία παρτίδα με οποιονδήποτε άλλον.
νάνοι, που τα ονόματά τους είναι Α, Β, Γ, Δ, Ε, Ζ και Η, έπαιξαν μεταξύ τους μερικές παρτίδες σκάκι. Ο καθένας έπαιξε το πολύ μία παρτίδα με οποιονδήποτε άλλον.  παρτίδα, ο Β έπαιξε
παρτίδα, ο Β έπαιξε  , ο Γ
, ο Γ  , ο Δ
, ο Δ  , ο Ε
, ο Ε  και ο Ζ έπαιξε
και ο Ζ έπαιξε  παρτίδες. Πόσες παρτίδες έπαιξε ο έβδομος νάνος και με ποιους;
παρτίδες. Πόσες παρτίδες έπαιξε ο έβδομος νάνος και με ποιους;
 αναγκαστικά έπαιξε με όλους τους νάνους εκτός τον εαυτό του.
αναγκαστικά έπαιξε με όλους τους νάνους εκτός τον εαυτό του. δεν μπορεί να έπαιξε με τον
δεν μπορεί να έπαιξε με τον  , λόγω του
, λόγω του  (και
(και  δεν μπορεί να έπαιξε με τον
δεν μπορεί να έπαιξε με τον  λόγω του
λόγω του  (και
(και  )
) έπαιξε
έπαιξε  και
και  ,
,  δυναμοσύνολο και *συνάρτηση
δυναμοσύνολο και *συνάρτηση  τέτοια, ώστε
τέτοια, ώστε






 και
και

 από
από  από
από  από
από  από
από  από
από  από
από  από
από  από
από  τέτοιο, ώστε
τέτοιο, ώστε  τότε
τότε  από
από 
 στο δυναμοσύνολό του με την ιδιότητα
στο δυναμοσύνολό του με την ιδιότητα 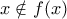 (για να δηλώσεις το αυτονόητο ότι κανείς δεν έπαιξε παρτίδα με τον εαυτό του) και
(για να δηλώσεις το αυτονόητο ότι κανείς δεν έπαιξε παρτίδα με τον εαυτό του) και 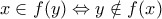 (για να δηλώσεις το αυτονόητο ότι αν ο
(για να δηλώσεις το αυτονόητο ότι αν ο  έπαιξε παρτίδα με τον
έπαιξε παρτίδα με τον  τότε και
τότε και  μετά
μετά  μετά
μετά  μετά
μετά  μετά
μετά  μετά
μετά  μετά
μετά 