Τετράπλευρο και ισόπλευρο τρίγωνο.

[Φανης Θεοφανιδης]

Τετράπλευρο και ισόπλευρο τρίγωνο..png (6.19 KiB) Προβλήθηκε 545 φορές

Στο παραπάνω σχήμα για το τετράπλευρο ισχύει ότι
και . Το τρίγωνο είναι ισόπλευρο.
Αποδείξτε ότι και το τρίγωνο , είναι επίσης ισόπλευρο.

[Ορέστης Λιγνός]

Τετράπλευρο και ισόπλευρο τρίγωνο..png

Στο παραπάνω σχήμα για το τετράπλευρο ισχύει ότι
και . Το τρίγωνο είναι ισόπλευρο.
Αποδείξτε ότι και το τρίγωνο , είναι επίσης ισόπλευρο.

Καλησπέρα!

Αφού το άθροισμα των γωνιών και είναι , πρέπει .
Αν λοιπόν , είναι ακόμη .

Έτσι, , συνεπώς τα τρίγωνα είναι ίσα, επομένως .
Επίσης, .

Από τις δύο τελευταίες σχέσεις, έπεται ότι το τρίγωνο είναι ισόπλευρο.

[Doloros]

Τετράπλευρο και ισόπλευρο τρίγωνο..png
Στο παραπάνω σχήμα για το τετράπλευρο ισχύει ότι
και . Το τρίγωνο είναι ισόπλευρο.
Αποδείξτε ότι και το τρίγωνο , είναι επίσης ισόπλευρο.

Το σημείο είναι το σημείο σταθερό και μάλιστα ο Βόρειος πόλος του κύκλου όπου το σημείο τομής των .

Το ζητούμενο έτσι φανερό.

Isopleyra.png (37.36 KiB) Προβλήθηκε 510 φορές

Θα δώσω όμως και στοιχειώδη λύση

Που τελικά την έδωσε Ο Ορέστης , όπως φαίνεται στο πιο πάνω σχήμα μου.



Αν το σημείο τομής των προφανώς η γωνία και έτσι το τετράπλευρο είναι εγγράψιμο .

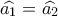Επειδή τώρα και τα παραπληρώματα τους θα είναι ίσα με άμεση συνέπεια

. Τώρα στο ισοσκελές τρίγωνο οι παρά τη βάση του γωνίες θα έχουν άθροισμα και άρα είναι ισόπλευρο.

Παρατήρηση.

Για το σημείο μπορείτε να βρείτε λεπτομέρειες στο Βιβλίο του Αρίστου Δημητρίου σελίδα 128 θέμα 16..


Φιλικά Νίκος