Το 1980 και το 1981 οι εισαγωγικές εξετάσεις για τους δύο τύπους λυκείων έγιναν σε μορφή πανελληνίων εξετάσεων.
Βρήκα τα θέματα του 1980 στο Δελτίο του Πάλλα εκείνης της χρονιάς. Αυτό ήταν και το τελευταίο δελτίο, έτσι δεν ξέρω πού μπορεί να υπάρχουν τα θέματα του 1981. Ίσως σε εφημερίδες της εποχής. Δημοσιεύω τα θέματα του 1980 και τονίζω ότι η δημοσίευση αυτή έχει ιστορικό χαρακτήρα.
ΓΕΝΙΚΟ ΛΥΚΕΙΟ
ΘΕΜΑ 1
Να επιλυθεί η εξίσωση

ΘΕΜΑ 2
Στο πολυώνυμο

να εκτελέσετε τις πράξεις, να κάνετε αναγωγή των ομοίων όρων και τέλος να βρείτε την αριθμητική τιμή του για

ΘΕΜΑ 3
Στο επίπεδο των ορθογωνίων αξόνων χΟψ η εξίσωση μιας ευθείας είναι

Nα βρείτε τις συντεταγμένες των σημείων στα οποία η ευθεία αυτή τέμνει τους άξονες.
ΘΕΜΑ 4
Να επιλυθεί το σύστημα:


ΤΕΧΝΙΚΟ-ΕΠΑΓΓΕΛΜΑΤΙΚΟ ΛΥΚΕΙΟ
ΘΕΜΑ 1
Να επιλυθεί η εξίσωση

ΘΕΜΑ 2
Δίδεται η παράστασις

Nα εκτελεστούν οι πράξεις και μετά να βρεθεί η αριθμητική τιμή αυτής για

ΘΕΜΑ 3
Να προσδιοριστεί το
 έτσι ώστε το πολυώνυμο
έτσι ώστε το πολυώνυμο 
να είναι διαιρετό με το διώνυμο

ΘΕΜΑ 4
Το πολυώνυμο
 να διαιρεθεί με το
να διαιρεθεί με τοπολυώνυμο
 και έπειτα να γίνει η επαλήθευση.
και έπειτα να γίνει η επαλήθευση.


 και
και  . Έχουμε διαδοχικά:
. Έχουμε διαδοχικά:

 .
. . Άρα, τέμνει τον άξονα
. Άρα, τέμνει τον άξονα 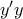 στο σημείο
στο σημείο  ενώ τον άξονα
ενώ τον άξονα  στο σημείο
στο σημείο  .
.
 είναι
είναι  .
.