parmenides51 έγραψε:
4. Να βρεθούν οι πραγματικές λύσεις της ανίσωσης
 5.
5. Να δειχθεί οτι η εξίσωση

έχει ρίζες πραγματικές όταν

4. Είναι:

.
Τα απόλυτα μηδενίζονται στο

αντίστοιχα. Οπότε θα δουλέψουμε στα διαστήματα

και στη συνέχεια θα κοιτάξουμε αν οι ρίζες επαληθεύουν την ανίσωση.
Για

συνεπώς η ανίσωση γίνεται:

. Επίσης πρέπει να είναι και

κατά συνέπεια είναι

.
Για

είναι

συνεπώς είναι:

και επειδή πρέπει

πρέπει τελικά να είναι

.
Για

είναι

και κατά συνέπεια είναι:

το οποίο ισχύει.
Για

ενώ για

.
Τέλος συναληθεύουμε όλους τους περιορισμούς και έχουμε πως η δοσμένη ανίσωση ισχύει

.
5. Μετά από λανθασμένη λύση και υπόδειξη, για τη κατανόηση της εκφώνησης την οποία παρερμήνευσα, από τον parmenides51 τον οποίο ευχαριστώ δίνω μία άλλη για την οποία ελπίζω να είμαι σωστός.
Θα δείξω ότι αν

τότε το τριώνυμο έχει πραγματικές ρίζες. Πράγματι έχουμε:

τότε το ελλειπτικό τριώνυμο έχει διακρίνουσα

εφόσον

το οποίο αποδεικνύει το ζητούμενο.
Τόλης
 , να δειχτεί οτι
, να δειχτεί οτι  .
. 
 να είναι συμβιβαστό, όταν
να είναι συμβιβαστό, όταν 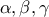 πραγματικοί και
πραγματικοί και  .
. είναι συμβιβαστό και να προσδιοριστούν τα
είναι συμβιβαστό και να προσδιοριστούν τα  .
.
 έχει ρίζες πραγματικές όταν
έχει ρίζες πραγματικές όταν 

 .
. αντίστοιχα. Οπότε θα δουλέψουμε στα διαστήματα
αντίστοιχα. Οπότε θα δουλέψουμε στα διαστήματα  και στη συνέχεια θα κοιτάξουμε αν οι ρίζες επαληθεύουν την ανίσωση.
και στη συνέχεια θα κοιτάξουμε αν οι ρίζες επαληθεύουν την ανίσωση. συνεπώς η ανίσωση γίνεται:
συνεπώς η ανίσωση γίνεται:  . Επίσης πρέπει να είναι και
. Επίσης πρέπει να είναι και  κατά συνέπεια είναι
κατά συνέπεια είναι  είναι
είναι  συνεπώς είναι:
συνεπώς είναι:  και επειδή πρέπει
και επειδή πρέπει  είναι
είναι  και κατά συνέπεια είναι:
και κατά συνέπεια είναι:  το οποίο ισχύει.
το οποίο ισχύει. ενώ για
ενώ για  .
. .
.  τότε το τριώνυμο έχει πραγματικές ρίζες. Πράγματι έχουμε:
τότε το τριώνυμο έχει πραγματικές ρίζες. Πράγματι έχουμε:  τότε το ελλειπτικό τριώνυμο έχει διακρίνουσα
τότε το ελλειπτικό τριώνυμο έχει διακρίνουσα  εφόσον
εφόσον  το οποίο αποδεικνύει το ζητούμενο.
το οποίο αποδεικνύει το ζητούμενο. 