Μαθηματικά ΓΕΛ 2025 (Θέματα & Λύσεις)
-
Επιτροπή Θεμάτων 2025
- Δημοσιεύσεις: 33
- Εγγραφή: Πέμ Μάιος 12, 2016 9:41 am
Μαθηματικά ΓΕΛ 2025 (Θέματα & Λύσεις)
Αγαπητές/τοί φίλες/οι
Στο θέμα αυτό θα αναρτηθούν (αμέσως μόλις δημοσιευθούν στη σελίδα του Υπουργείου) και, αποκλειστικά, θα λυθούν τα θέματα των Μαθηματικών 2025 (των ημερησίων ΓΕΛ). Επομένως σχολιασμοί-κριτική επί της δυσκολίας κ.λ.π. των θεμάτων θα απομακρύνονται από αυτήν την συζήτηση. Αυτές μπορούν να γίνουν στο Σχόλια στα Μαθηματικά ΓΕΛ 2025.
Στο θέμα αυτό θα αναρτηθούν (αμέσως μόλις δημοσιευθούν στη σελίδα του Υπουργείου) και, αποκλειστικά, θα λυθούν τα θέματα των Μαθηματικών 2025 (των ημερησίων ΓΕΛ). Επομένως σχολιασμοί-κριτική επί της δυσκολίας κ.λ.π. των θεμάτων θα απομακρύνονται από αυτήν την συζήτηση. Αυτές μπορούν να γίνουν στο Σχόλια στα Μαθηματικά ΓΕΛ 2025.
Λέξεις Κλειδιά:
- polysot
- Επιμελητής
- Δημοσιεύσεις: 2601
- Εγγραφή: Δευ Οκτ 19, 2009 11:43 pm
- Τοποθεσία: Όπου βρω ενδιαφέρουσες προσωπικότητες...
- Επικοινωνία:
Re: Μαθηματικά ΓΕΛ 2025 (Θέματα & Λύσεις)
Γ1.
Η είναι συνεχής στο μηδέν καθώς ισχύει: \\
είναι συνεχής στο μηδέν καθώς ισχύει: \\
 και\\
και\\

Η δεν είναι παραγωγίσιμη στο 0, διότι:
δεν είναι παραγωγίσιμη στο 0, διότι:

ενώ

Η
 είναι συνεχής στο μηδέν καθώς ισχύει: \\
είναι συνεχής στο μηδέν καθώς ισχύει: \\ και\\
και\\
Η
 δεν είναι παραγωγίσιμη στο 0, διότι:
δεν είναι παραγωγίσιμη στο 0, διότι:
ενώ

Σωτήρης Δ. Χασάπης
Ζήσε τα μαθηματικά σου!
-----------------------------
"There is a scientific taste just as there is a literary or artistic one", Renan
"The journey of a thousand miles begins with one step.", Lao Tzu
Ζήσε τα μαθηματικά σου!
-----------------------------
"There is a scientific taste just as there is a literary or artistic one", Renan
"The journey of a thousand miles begins with one step.", Lao Tzu
- polysot
- Επιμελητής
- Δημοσιεύσεις: 2601
- Εγγραφή: Δευ Οκτ 19, 2009 11:43 pm
- Τοποθεσία: Όπου βρω ενδιαφέρουσες προσωπικότητες...
- Επικοινωνία:
Re: Μαθηματικά ΓΕΛ 2025 (Θέματα & Λύσεις)
Γ2.
Εφόσον η συνάρτηση είναι συνεχής στο δεν έχει κατακόρυφες ασύμπτωτες.
δεν έχει κατακόρυφες ασύμπτωτες.
Για πλάγιες ασύμπτωτες στο έχουμε:
έχουμε:


οπότε η είναι πλάγια ασύμπτωτη της
είναι πλάγια ασύμπτωτη της  στο
στο  .
.
Για πλάγιες ασύμπτωτες στο έχουμε:
έχουμε:

Οπότε αναζητούμε οριζόντια ασύμπτωτη στο
 , διότι
, διότι
 , οπότε:
, οπότε:

και από κριτήριο παρεμβολής .
.
Συνεπώς, η οριζόντια ασύμπτωτη της
οριζόντια ασύμπτωτη της  στο
στο  .
.
Εφόσον η συνάρτηση είναι συνεχής στο
 δεν έχει κατακόρυφες ασύμπτωτες.
δεν έχει κατακόρυφες ασύμπτωτες.Για πλάγιες ασύμπτωτες στο
 έχουμε:
έχουμε: 

οπότε η
 είναι πλάγια ασύμπτωτη της
είναι πλάγια ασύμπτωτη της  στο
στο  .
.Για πλάγιες ασύμπτωτες στο
 έχουμε:
έχουμε: 
Οπότε αναζητούμε οριζόντια ασύμπτωτη στο

 , διότι
, διότι , οπότε:
, οπότε:
και από κριτήριο παρεμβολής
 .
.Συνεπώς, η
 οριζόντια ασύμπτωτη της
οριζόντια ασύμπτωτη της  στο
στο  .
.Σωτήρης Δ. Χασάπης
Ζήσε τα μαθηματικά σου!
-----------------------------
"There is a scientific taste just as there is a literary or artistic one", Renan
"The journey of a thousand miles begins with one step.", Lao Tzu
Ζήσε τα μαθηματικά σου!
-----------------------------
"There is a scientific taste just as there is a literary or artistic one", Renan
"The journey of a thousand miles begins with one step.", Lao Tzu
- polysot
- Επιμελητής
- Δημοσιεύσεις: 2601
- Εγγραφή: Δευ Οκτ 19, 2009 11:43 pm
- Τοποθεσία: Όπου βρω ενδιαφέρουσες προσωπικότητες...
- Επικοινωνία:
Re: Μαθηματικά ΓΕΛ 2025 (Θέματα & Λύσεις)
\textbf{Γ3.}
Αρκεί η εξίσωση να έχει τουλάχιστον μία λύση στο διάστημα
να έχει τουλάχιστον μία λύση στο διάστημα 
Θεωρούμε τη συνάρτηση , η οποία είναι συνεχής στο διάστημα
, η οποία είναι συνεχής στο διάστημα ![[-\pi, 0] [-\pi, 0]](/forum/ext/geomar/texintegr/latexrender/pictures/f92fce7cbe481198577892cdabf66462.png) και ισχύουν:
και ισχύουν:


οπότε από Θεώρημα Bolzano υπάρχει τουλάχιστον ένα έτσι ώστε
έτσι ώστε 
απ' όπου προκύπτει το ζητούμενο.
Αρκεί η εξίσωση
 να έχει τουλάχιστον μία λύση στο διάστημα
να έχει τουλάχιστον μία λύση στο διάστημα 
Θεωρούμε τη συνάρτηση
 , η οποία είναι συνεχής στο διάστημα
, η οποία είναι συνεχής στο διάστημα ![[-\pi, 0] [-\pi, 0]](/forum/ext/geomar/texintegr/latexrender/pictures/f92fce7cbe481198577892cdabf66462.png) και ισχύουν:
και ισχύουν: 

οπότε από Θεώρημα Bolzano υπάρχει τουλάχιστον ένα
 έτσι ώστε
έτσι ώστε 
απ' όπου προκύπτει το ζητούμενο.
Σωτήρης Δ. Χασάπης
Ζήσε τα μαθηματικά σου!
-----------------------------
"There is a scientific taste just as there is a literary or artistic one", Renan
"The journey of a thousand miles begins with one step.", Lao Tzu
Ζήσε τα μαθηματικά σου!
-----------------------------
"There is a scientific taste just as there is a literary or artistic one", Renan
"The journey of a thousand miles begins with one step.", Lao Tzu
Re: Μαθηματικά ΓΕΛ 2025 (Θέματα & Λύσεις)
Δ1. Παρατηρούμε ότι για  ,
,

Άρα η είναι σταθερή.
είναι σταθερή.
Δ2. Με στη δοθείσα παίρνουμε
στη δοθείσα παίρνουμε  και από τη συνθήκη της εφαπτομένης
και από τη συνθήκη της εφαπτομένης  . Άρα
. Άρα

από L'Hospital. Έτσι

Είναι

Αφού η είναι σταθερή , είναι
είναι σταθερή , είναι  για κάθε
για κάθε  , οπότε
, οπότε  για κάθε
για κάθε  .
.
Δ3. Είναι
για .
.
Έτσι, διακρίνοντας περιπτώσεις βλέπουμε ότι αφού για
για  έχουμε αν
έχουμε αν  είναι
είναι  , ενώ αν
, ενώ αν  , τότε
, τότε  .
.
Άρα η είναι γν. αύξουσα στο
είναι γν. αύξουσα στο  και γν.φθίνουσα στο
και γν.φθίνουσα στο ![(0,1] (0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/668c7b55a37300c330dcd565d9e076da.png) .
.
Προφανώς μια λύση της δοθείσας εξίσωσης είναι η
είναι η  .
.
Έπειτα, αν , τότε
, τότε  , οπότε, λόγω μονοτονίας,
, οπότε, λόγω μονοτονίας,  ενώ αν
ενώ αν  , τότε
, τότε  οπότε
οπότε  .
.
Σε κάθε περίπτωση, αν , τότε
, τότε  . Άρα η δοθείσα εξίσωση έχει μοναδική λύση
. Άρα η δοθείσα εξίσωση έχει μοναδική λύση  .
.
Δ4. Αφού για κάθε
για κάθε  και
και  για κάθε
για κάθε  με το "=" αν-ν
με το "=" αν-ν  έχουμε
έχουμε

Φιλικά,
Αχιλλέας
 ,
, 
Άρα η
 είναι σταθερή.
είναι σταθερή.Δ2. Με
 στη δοθείσα παίρνουμε
στη δοθείσα παίρνουμε  και από τη συνθήκη της εφαπτομένης
και από τη συνθήκη της εφαπτομένης  . Άρα
. Άρα
από L'Hospital. Έτσι

Είναι

Αφού η
 είναι σταθερή , είναι
είναι σταθερή , είναι  για κάθε
για κάθε  , οπότε
, οπότε  για κάθε
για κάθε  .
.Δ3. Είναι

για
 .
. Έτσι, διακρίνοντας περιπτώσεις βλέπουμε ότι αφού
 για
για  έχουμε αν
έχουμε αν  είναι
είναι  , ενώ αν
, ενώ αν  , τότε
, τότε  .
.Άρα η
 είναι γν. αύξουσα στο
είναι γν. αύξουσα στο  και γν.φθίνουσα στο
και γν.φθίνουσα στο ![(0,1] (0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/668c7b55a37300c330dcd565d9e076da.png) .
. Προφανώς μια λύση της δοθείσας εξίσωσης
 είναι η
είναι η  .
.Έπειτα, αν
 , τότε
, τότε  , οπότε, λόγω μονοτονίας,
, οπότε, λόγω μονοτονίας,  ενώ αν
ενώ αν  , τότε
, τότε  οπότε
οπότε  .
.Σε κάθε περίπτωση, αν
 , τότε
, τότε  . Άρα η δοθείσα εξίσωση έχει μοναδική λύση
. Άρα η δοθείσα εξίσωση έχει μοναδική λύση  .
.Δ4. Αφού
 για κάθε
για κάθε  και
και  για κάθε
για κάθε  με το "=" αν-ν
με το "=" αν-ν  έχουμε
έχουμε
Φιλικά,
Αχιλλέας
- polysot
- Επιμελητής
- Δημοσιεύσεις: 2601
- Εγγραφή: Δευ Οκτ 19, 2009 11:43 pm
- Τοποθεσία: Όπου βρω ενδιαφέρουσες προσωπικότητες...
- Επικοινωνία:
Re: Μαθηματικά ΓΕΛ 2025 (Θέματα & Λύσεις)
Γ4.
Ισχύει ότι
Επιπλέον και
και

Αναζητείται λύση της εξίσωσης:


το οποίο είναι αδύνατο.
Συνεπώς δεν υπάρχει τέτοιο .
.
Ισχύει ότι

Επιπλέον
 και
και 
Αναζητείται λύση της εξίσωσης:


το οποίο είναι αδύνατο.
Συνεπώς δεν υπάρχει τέτοιο
 .
.Σωτήρης Δ. Χασάπης
Ζήσε τα μαθηματικά σου!
-----------------------------
"There is a scientific taste just as there is a literary or artistic one", Renan
"The journey of a thousand miles begins with one step.", Lao Tzu
Ζήσε τα μαθηματικά σου!
-----------------------------
"There is a scientific taste just as there is a literary or artistic one", Renan
"The journey of a thousand miles begins with one step.", Lao Tzu
-
thepigod762
- Δημοσιεύσεις: 94
- Εγγραφή: Σάβ Οκτ 23, 2021 1:02 am
- Τοποθεσία: Λάρισα
Re: Μαθηματικά ΓΕΛ 2025 (Θέματα & Λύσεις)
Καλησπέρα, συγγνώμη, θέλω να ρωτήσω αν η αντικατάσταση u=lnx όπου καταλήγω στο e^u^2+u και χρησιμοποιώ την e^u^2+u >= u^2+u+1 είναι σωστή, γιατί καταλήγει σε ένα αποτέλεσμα με πολυώνυμο τρίτου βαθμού. Κατά τη διάρκεια της εξέτασης έτσι το δικαιολόγησα και πίστεψα ότι είναι εντάξει. Θα μου το πάρουν σωστό;
Γιώργος Κοτσάλης
Re: Μαθηματικά ΓΕΛ 2025 (Θέματα & Λύσεις)
Αν κατάλαβα σωστά την αλλαγή μεταβλητής, τότε αλλάζουν τα όρια ολοκλήρωσης από 0 έως 1.thepigod762 έγραψε: ↑Δευ Ιουν 02, 2025 2:10 pmΚαλησπέρα, συγγνώμη, θέλω να ρωτήσω αν η αντικατάσταση u=lnx όπου καταλήγω στο e^u^2+u και χρησιμοποιώ την e^u^2+u >= u^2+u+1 είναι σωστή, γιατί καταλήγει σε ένα αποτέλεσμα με πολυώνυμο τρίτου βαθμού. Κατά τη διάρκεια της εξέτασης έτσι το δικαιολόγησα και πίστεψα ότι είναι εντάξει. Θα μου το πάρουν σωστό;
Το ολοκλήρωμα

-
thepigod762
- Δημοσιεύσεις: 94
- Εγγραφή: Σάβ Οκτ 23, 2021 1:02 am
- Τοποθεσία: Λάρισα
Re: Μαθηματικά ΓΕΛ 2025 (Θέματα & Λύσεις)
Σωστά, αλλάζουν τα όρια ολοκλήρωσης. Αβλεψία, ευχαριστώachilleas έγραψε: ↑Δευ Ιουν 02, 2025 2:31 pmΑν κατάλαβα σωστά την αλλαγή μεταβλητής, τότε αλλάζουν τα όρια ολοκλήρωσης από 0 έως 1.thepigod762 έγραψε: ↑Δευ Ιουν 02, 2025 2:10 pmΚαλησπέρα, συγγνώμη, θέλω να ρωτήσω αν η αντικατάσταση u=lnx όπου καταλήγω στο e^u^2+u και χρησιμοποιώ την e^u^2+u >= u^2+u+1 είναι σωστή, γιατί καταλήγει σε ένα αποτέλεσμα με πολυώνυμο τρίτου βαθμού. Κατά τη διάρκεια της εξέτασης έτσι το δικαιολόγησα και πίστεψα ότι είναι εντάξει. Θα μου το πάρουν σωστό;
Το ολοκλήρωμα
Γιώργος Κοτσάλης
Re: Μαθηματικά ΓΕΛ 2025 (Θέματα & Λύσεις)
thepigod762 έγραψε: ↑Δευ Ιουν 02, 2025 2:34 pmΣωστά, αλλάζουν τα όρια ολοκλήρωσης. Αβλεψία, ευχαριστώachilleas έγραψε: ↑Δευ Ιουν 02, 2025 2:31 pmΑν κατάλαβα σωστά την αλλαγή μεταβλητής, τότε αλλάζουν τα όρια ολοκλήρωσης από 0 έως 1.thepigod762 έγραψε: ↑Δευ Ιουν 02, 2025 2:10 pmΚαλησπέρα, συγγνώμη, θέλω να ρωτήσω αν η αντικατάσταση u=lnx όπου καταλήγω στο e^u^2+u και χρησιμοποιώ την e^u^2+u >= u^2+u+1 είναι σωστή, γιατί καταλήγει σε ένα αποτέλεσμα με πολυώνυμο τρίτου βαθμού. Κατά τη διάρκεια της εξέτασης έτσι το δικαιολόγησα και πίστεψα ότι είναι εντάξει. Θα μου το πάρουν σωστό;
Το ολοκλήρωμα
Πάντως, η ιδέα σου είναι καλή, καθώς οδηγεί σε ολοκλήρωμα που θα λέγαμε ότι είναι πιο εύκολο να υπολογιστεί. Αρκεί να μην εφαρμόσει κάποιος την ανισότητα σε όλη την υπο-ολοκλήρωση συνάρτηση:

-
thepigod762
- Δημοσιεύσεις: 94
- Εγγραφή: Σάβ Οκτ 23, 2021 1:02 am
- Τοποθεσία: Λάρισα
Re: Μαθηματικά ΓΕΛ 2025 (Θέματα & Λύσεις)
Κατάλαβα, ωραία λύση!achilleas έγραψε: ↑Δευ Ιουν 02, 2025 2:50 pmthepigod762 έγραψε: ↑Δευ Ιουν 02, 2025 2:34 pmΣωστά, αλλάζουν τα όρια ολοκλήρωσης. Αβλεψία, ευχαριστώachilleas έγραψε: ↑Δευ Ιουν 02, 2025 2:31 pmΑν κατάλαβα σωστά την αλλαγή μεταβλητής, τότε αλλάζουν τα όρια ολοκλήρωσης από 0 έως 1.thepigod762 έγραψε: ↑Δευ Ιουν 02, 2025 2:10 pmΚατάλαβα, ωραία λύση!
Μπορεί να μην δίνει το ζητούμενο αποτέλεσμα, αλλά να σημειώσω ότι μπορεί κάποιος να οδηγηθεί σε φράξιμο αν εφαρμόσει παραγοντική με το (Χ)', και έπειτα στο ολοκλήρωμα xf(x) αν χρησιμοποιήσω τη σχέση καταλήγω στο 2F(x)lnx . Και στο F(x)lnx αν χρησιμοποιήσω lnx<=1 παίρνω τελικά ότι το ολοκλήρωμα της F(x) είναι μεγαλύτερο από (e^2-1)/3. Όμως αν ήθελα να έχω το ζητούμενο θα έπρεπε e^2-6e+8>0, που όμως δεν ισχύει καθώς e ε (2, 4). Αυτό για να δείξω σε τι δρόμους μπορεί να καταλήξει ο μαθητής...
Το ολοκλήρωμα
Πάντως, η ιδέα σου είναι καλή, καθώς οδηγεί σε ολοκλήρωμα που θα λέγαμε ότι είναι πιο εύκολο να υπολογιστεί. Αρκεί να μην εφαρμόσει κάποιος την ανισότητα σε όλη την υπο-ολοκλήρωση συνάρτηση:

Μπορεί να μην δίνει το ζητούμενο αποτέλεσμα, αλλά να σημειώσω ότι μπορεί κάποιος να οδηγηθεί σε φράξιμο αν εφαρμόσει παραγοντική με το (Χ)', και έπειτα στο ολοκλήρωμα F(x)lnx που απομένει αν χρησιμοποιήσω lnx<=1 παίρνω τελικά ότι το ολοκλήρωμα της F(x) είναι μεγαλύτερο από (e^2-1)/3. Όμως αν ήθελα να έχω το ζητούμενο θα έπρεπε e^2-6e+8>0, που όμως δεν ισχύει καθώς e ε (2, 4). Αυτό για να δείξω σε τι δρόμους μπορεί να καταλήξει ο μαθητής...
Γιώργος Κοτσάλης
Re: Μαθηματικά ΓΕΛ 2025 (Θέματα & Λύσεις)
Αν θελήσουμε να πετύχουμε όσο δυνατόν το βέλτιστο παίρνουμε το ολοκλήρωμα που είπε ο Γιώργος και από την  για θετικό ακέραιο
για θετικό ακέραιο  και βάζοντας n=3 παίρνουμε το ζητούμενο.
και βάζοντας n=3 παίρνουμε το ζητούμενο.
Στο λέω φιλικά Γιώργο, ώστε αν δεν φτάσουν οι πρώτοι δύο όροι να έχεις κι άλλους μετά.
 για θετικό ακέραιο
για θετικό ακέραιο  και βάζοντας n=3 παίρνουμε το ζητούμενο.
και βάζοντας n=3 παίρνουμε το ζητούμενο.Στο λέω φιλικά Γιώργο, ώστε αν δεν φτάσουν οι πρώτοι δύο όροι να έχεις κι άλλους μετά.
Re: Μαθηματικά ΓΕΛ 2025 (Θέματα & Λύσεις)
Δ4. Αλλιώς:
Ισχύει για κάθε
για κάθε 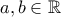 λόγω κυρτότητας(*) της
λόγω κυρτότητας(*) της  και
και
 , αφού είναι ισοδύναμη με
, αφού είναι ισοδύναμη με  .
.
Άρα, αν , τότε
, τότε
 ,
,
οπότε

για κάθε με το "=" αν και μόνο αν
με το "=" αν και μόνο αν  .
.
Επίσης, για κάθε
για κάθε 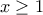 και
και  .
.
Έτσι, όπως φαίνεται στο παρακάτω σχήμα, όπου (αφού
(αφού  αν και μόνο αν
αν και μόνο αν  ) και
) και  είναι
είναι

(αφού που ισχύει για
που ισχύει για  ).
).
*Σημείωση-Σχόλιο. Η ανισότητα αυτή αποδεικνύεται στοιχειωδώς, αφού διαιρώντας και τα δύο μέλη με βλέπουμε ότι είναι ισοδύναμη με την
βλέπουμε ότι είναι ισοδύναμη με την
 ,
,
η οποία ισχύει, με το "=" αν-ν .
.
Ισχύει
 για κάθε
για κάθε 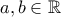 λόγω κυρτότητας(*) της
λόγω κυρτότητας(*) της  και
και  , αφού είναι ισοδύναμη με
, αφού είναι ισοδύναμη με  .
.Άρα, αν
 , τότε
, τότε ,
, οπότε

για κάθε
 με το "=" αν και μόνο αν
με το "=" αν και μόνο αν  .
.Επίσης,
 για κάθε
για κάθε 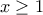 και
και  .
. Έτσι, όπως φαίνεται στο παρακάτω σχήμα, όπου
 (αφού
(αφού  αν και μόνο αν
αν και μόνο αν  ) και
) και  είναι
είναι
(αφού
 που ισχύει για
που ισχύει για  ).
).*Σημείωση-Σχόλιο. Η ανισότητα αυτή αποδεικνύεται στοιχειωδώς, αφού διαιρώντας και τα δύο μέλη με
 βλέπουμε ότι είναι ισοδύναμη με την
βλέπουμε ότι είναι ισοδύναμη με την ,
, η οποία ισχύει, με το "=" αν-ν
 .
.- Συνημμένα
-
- Δ4_b.png (43.13 KiB) Προβλήθηκε 5283 φορές
Re: Μαθηματικά ΓΕΛ 2025 (Θέματα & Λύσεις)
Ανεβάζω τα θέματα σε word για διευκόλυνση του Σωτήρη
Γιατί πάντα αριθμόν έχοντι. Άνευ τούτου ουδέν νοητόν και γνωστόν.
Δ4 Μια λύση heavy metal
Η  στο
στο ![[1,e] [1,e]](/forum/ext/geomar/texintegr/latexrender/pictures/84b8350dcaf54462dc964cf2fca7f6c0.png) άρα η εφαπτόμενη ''από κάτω''.
άρα η εφαπτόμενη ''από κάτω''.
Η εφαπτόμενη στο είναι
είναι  και τέμνει την
και τέμνει την  , εφαπτόμενη στο
, εφαπτόμενη στο  στο
στο  . Η
. Η  τέμνει την
τέμνει την  στο
στο 
Το ορθογώνιο με διαστάσεις e-1, 1 και το τρίγωνο με βάση DF και ύψος FB έχουν μαζί εμβαδόν μεγαλύτερο του
μεγαλύτερο του  αφού ισχύει η ανίσωση και το ζητούμενο εμβαδόν είναι μεγαλύτερο του αθροίσματος εμβαδών ορθογώνιου και τριγώνου
αφού ισχύει η ανίσωση και το ζητούμενο εμβαδόν είναι μεγαλύτερο του αθροίσματος εμβαδών ορθογώνιου και τριγώνου
Θα βάλω λίγο αργότερα και τους λογαριασμούς για να γίνει φανερό
 στο
στο ![[1,e] [1,e]](/forum/ext/geomar/texintegr/latexrender/pictures/84b8350dcaf54462dc964cf2fca7f6c0.png) άρα η εφαπτόμενη ''από κάτω''.
άρα η εφαπτόμενη ''από κάτω''.Η εφαπτόμενη στο
 είναι
είναι  και τέμνει την
και τέμνει την  , εφαπτόμενη στο
, εφαπτόμενη στο  στο
στο  . Η
. Η  τέμνει την
τέμνει την  στο
στο 
Το ορθογώνιο με διαστάσεις e-1, 1 και το τρίγωνο με βάση DF και ύψος FB έχουν μαζί εμβαδόν
 μεγαλύτερο του
μεγαλύτερο του  αφού ισχύει η ανίσωση και το ζητούμενο εμβαδόν είναι μεγαλύτερο του αθροίσματος εμβαδών ορθογώνιου και τριγώνου
αφού ισχύει η ανίσωση και το ζητούμενο εμβαδόν είναι μεγαλύτερο του αθροίσματος εμβαδών ορθογώνιου και τριγώνουΘα βάλω λίγο αργότερα και τους λογαριασμούς για να γίνει φανερό
τελευταία επεξεργασία από venpan σε Τρί Ιουν 03, 2025 12:17 pm, έχει επεξεργασθεί 3 φορές συνολικά.
Re: Δ4 Μια λύση heavy metal
Την ανέφερα χτες στην συνάντηση των εποπτών. Το ανέβασμα του σχήματος μου έκανε κάτι νερά...
Re: Μαθηματικά ΓΕΛ 2025 (Θέματα & Λύσεις)
Η λύση μου στο θεμα Δ διαφερει καπως....
Δ1

Δ2



Δ3
 γνησίως φθίνουσα στο
γνησίως φθίνουσα στο ![\displaystyle \left( 0, 1\right] \displaystyle \left( 0, 1\right]](/forum/ext/geomar/texintegr/latexrender/pictures/1167152b857ce9428e469f07099abe3a.png) και γνησίως αύξουσα στο
και γνησίως αύξουσα στο 


Λύση μόνο
Δ4
Από τη συνέχεια της συνάρτησης στο κλειστό διάστημα αυτό κι επειδή είναι θετική σε αυτό πάμε στο αποδεικτέο που ισοδυναμεί με
![\displaystyle \int_{0}^{1}\left( 1+u+u^{2}+\frac{\left( u^{2}+u \right)^{2}}{2}+\frac{\left( u^{2} +u\right)^{3}}{6} \right)du=\left[ u+\frac{u^{2}}{2}+\frac{u^{3}}{2}+\frac{7u^{4}}{24} +\frac{u^{5}}{5}+\frac{u^{6}}{12}+\frac{u^{7}}{42}\right]^{1}_{0} \displaystyle \int_{0}^{1}\left( 1+u+u^{2}+\frac{\left( u^{2}+u \right)^{2}}{2}+\frac{\left( u^{2} +u\right)^{3}}{6} \right)du=\left[ u+\frac{u^{2}}{2}+\frac{u^{3}}{2}+\frac{7u^{4}}{24} +\frac{u^{5}}{5}+\frac{u^{6}}{12}+\frac{u^{7}}{42}\right]^{1}_{0}](/forum/ext/geomar/texintegr/latexrender/pictures/00fe476458b1c2fc7e1c61ab2a5e3794.png)
Αυτό είναι μεγαλύτερο από το λόγω της
λόγω της  το οποίο κάνοντας μια κάθετη διαίρεση και έχοντας στο μυαλό μας ότι
το οποίο κάνοντας μια κάθετη διαίρεση και έχοντας στο μυαλό μας ότι  είναι άμεσο.
είναι άμεσο.
Από την γνωστή
λόγω της
τελειώσαμε.
Υπάρχει κι άλλη λύση που είναι δική μου και δεν έχει δοθεί πουθενά (δεν είναι μομφή αυτό προς κάποιον) και είναι σχολική. Θα την βάλω όποτε πάψει να με κάνει το latex να υποφέρω.
Δ1

Δ2



Δ3
 γνησίως φθίνουσα στο
γνησίως φθίνουσα στο ![\displaystyle \left( 0, 1\right] \displaystyle \left( 0, 1\right]](/forum/ext/geomar/texintegr/latexrender/pictures/1167152b857ce9428e469f07099abe3a.png) και γνησίως αύξουσα στο
και γνησίως αύξουσα στο 


Λύση μόνο

Δ4
Από τη συνέχεια της συνάρτησης στο κλειστό διάστημα αυτό κι επειδή είναι θετική σε αυτό πάμε στο αποδεικτέο που ισοδυναμεί με

![\displaystyle \int_{0}^{1}\left( 1+u+u^{2}+\frac{\left( u^{2}+u \right)^{2}}{2}+\frac{\left( u^{2} +u\right)^{3}}{6} \right)du=\left[ u+\frac{u^{2}}{2}+\frac{u^{3}}{2}+\frac{7u^{4}}{24} +\frac{u^{5}}{5}+\frac{u^{6}}{12}+\frac{u^{7}}{42}\right]^{1}_{0} \displaystyle \int_{0}^{1}\left( 1+u+u^{2}+\frac{\left( u^{2}+u \right)^{2}}{2}+\frac{\left( u^{2} +u\right)^{3}}{6} \right)du=\left[ u+\frac{u^{2}}{2}+\frac{u^{3}}{2}+\frac{7u^{4}}{24} +\frac{u^{5}}{5}+\frac{u^{6}}{12}+\frac{u^{7}}{42}\right]^{1}_{0}](/forum/ext/geomar/texintegr/latexrender/pictures/00fe476458b1c2fc7e1c61ab2a5e3794.png)
Αυτό είναι μεγαλύτερο από το
 λόγω της
λόγω της  το οποίο κάνοντας μια κάθετη διαίρεση και έχοντας στο μυαλό μας ότι
το οποίο κάνοντας μια κάθετη διαίρεση και έχοντας στο μυαλό μας ότι  είναι άμεσο.
είναι άμεσο. Από την γνωστή

λόγω της

τελειώσαμε.
Υπάρχει κι άλλη λύση που είναι δική μου και δεν έχει δοθεί πουθενά (δεν είναι μομφή αυτό προς κάποιον) και είναι σχολική. Θα την βάλω όποτε πάψει να με κάνει το latex να υποφέρω.
Re: Μαθηματικά ΓΕΛ 2025 (Θέματα & Λύσεις)
ΘΕΜΑ Γ
Γ1
Κοντά στο
Κοντά στο
από εδώ έχουμε τη συνέχεια στο μηδέν και επειδή κοντά στο απορρίπτεται η παραγωγισιμότητα στο μηδέν.
απορρίπτεται η παραγωγισιμότητα στο μηδέν.
Γ2
Από τη συνέχεια της συνάρτησης στο σύνολο των αρνητικών ως γινόμενο εκθετικής και ημιτονοειδούς και από τη συνέχεια της συνάρτησης στο σύνολο των θετικών πραγματικών ως τετραγωνική ρίζα πολυωνυμικής και άρα συνεχούς συνάρτησης, λόγω της συνέχειάς της και στο μηδέν, θα είναι συνεχής στους πραγματικούς αριθμούς. Άρα η γραφική της παράσταση δεν έχει κατακόρυφες ασύμπτωτες.
Στέλνοντας
Άρα ο άξονας των τετμημένων είναι οριζόντια ασύμπτωτη της γραφικής παράστασης στο μείον άπειρο, οπότε δεν γίνεται να έχει και πλάγια ασύμπτωτη στο μείον άπειρο.
Στέλνοντας
Στέλνοντας
λόγω του Κανόνα De L' Hospital.
Οπότε πλάγια ασύμπτωτη στο συν άπειρο η και δεν έχει οριζόντια ασύμπτωτη στο συν άπειρο.
και δεν έχει οριζόντια ασύμπτωτη στο συν άπειρο.
Γ3 Κάντε έναν Bolazno είναι κλασική άσκηση.
Γ4. η συνάρτηση f είναι μη παραγωγίσιμη στο 0 οπότε μόνο την χρονική στιγμή 0 δεν ορίζεται ρυθμός μεταβολής των τεταγμένων του σημείου
Για τα θετικά t

Αλλιώς το Δ4

Από εδώ έχουμε ότι είναι κυρτή η προς ολοκλήρωση συνάρτηση.
Για κάθε x,y στο [1,e] ισχύει με ισότητα μόνο όταν x=y
με ισότητα μόνο όταν x=y
Από εδώ![\displaystyle \int_{1}^{e}F\left( x \right)dx> \int_{1}^{e}\left( y^{\ln y}-2y^{\ln y}\ln y+2y^{\ln y}\frac{\ln y}{y} x\right)dx=y^{\ln y}\left[\left( 1-2\ln y \right)x+x^{2}\frac{\ln y}{y} \right]^{e}_{1}= \displaystyle \int_{1}^{e}F\left( x \right)dx> \int_{1}^{e}\left( y^{\ln y}-2y^{\ln y}\ln y+2y^{\ln y}\frac{\ln y}{y} x\right)dx=y^{\ln y}\left[\left( 1-2\ln y \right)x+x^{2}\frac{\ln y}{y} \right]^{e}_{1}=](/forum/ext/geomar/texintegr/latexrender/pictures/d167bbb03df00dd0b0a643347daa0a8e.png)
![\displaystyle =y^{\ln y}\left[ \left( e-1 \right)\left( 1-2\ln y \right)+\left( e-1 \right)\left( e+1 \right)\frac{\ln y}{y} \right]=\left( e-1 \right)y^{\ln y}\left( 1-2\ln y+\left( e+1 \right) \frac{\ln y}{y}\right) \displaystyle =y^{\ln y}\left[ \left( e-1 \right)\left( 1-2\ln y \right)+\left( e-1 \right)\left( e+1 \right)\frac{\ln y}{y} \right]=\left( e-1 \right)y^{\ln y}\left( 1-2\ln y+\left( e+1 \right) \frac{\ln y}{y}\right)](/forum/ext/geomar/texintegr/latexrender/pictures/7e21301fb5e7c50f71e91b0289613e5f.png)
Θεωρούμε τη συνάρτηση ορισμένη στο [1,e]
ορισμένη στο [1,e]
Η h είναι παραγωγίσιμη στο [1,e] με
που είναι ομόσημη του
Παίρνουμε την στο [1,e] που με παραγώγους είναι άμεσο ότι είναι γνησίως φθίνουσα. Είναι όμως και συνεχής οπότε
στο [1,e] που με παραγώγους είναι άμεσο ότι είναι γνησίως φθίνουσα. Είναι όμως και συνεχής οπότε ![w\left([1,e]\right)=\left[w\left( e \right),w\left( 1\right)\right]=\left[ -2e,e-1 \right] w\left([1,e]\right)=\left[w\left( e \right),w\left( 1\right)\right]=\left[ -2e,e-1 \right]](/forum/ext/geomar/texintegr/latexrender/pictures/f78b8adddb807493e9b59b2e8643cef3.png) οπότε έχει ρίζα μάλιστα μοναδική λόγω γνήσιας μονοτονίας έστω
οπότε έχει ρίζα μάλιστα μοναδική λόγω γνήσιας μονοτονίας έστω 
Στο [1,ρ) ισχύει
Στο (ρ,e] ισχύει
και με συνεχή στο
συνεχή στο  η h είναι γνησίως αύξουσα στο [1,ρ] και γνησίως φθίνουσα στο [ρ,e] και επειδή είναι συνεχής ισχύει
η h είναι γνησίως αύξουσα στο [1,ρ] και γνησίως φθίνουσα στο [ρ,e] και επειδή είναι συνεχής ισχύει ![\displaystyle h\left( \left[ 1,p \right] \right)=\left[ h\left( 1 \right),h\left( p \right) \right]=\left[\frac{1}{e-1}-1,h\left(p \right) \right] \displaystyle h\left( \left[ 1,p \right] \right)=\left[ h\left( 1 \right),h\left( p \right) \right]=\left[\frac{1}{e-1}-1,h\left(p \right) \right]](/forum/ext/geomar/texintegr/latexrender/pictures/0a1c1b385e7b654706b19784caf7d21e.png) και
και ![\displaystyle h\left( \left[ p,e \right] \right)=\left[ h\left( e \right),h\left( p \right) \right]=\left[ \frac{e+1}{e}+\frac{1}{e-1}-3,h\left( p \right) \right] \displaystyle h\left( \left[ p,e \right] \right)=\left[ h\left( e \right),h\left( p \right) \right]=\left[ \frac{e+1}{e}+\frac{1}{e-1}-3,h\left( p \right) \right]](/forum/ext/geomar/texintegr/latexrender/pictures/adb59eea81fe2ec79f2385b04cdd1cfd.png)
Άρα το σύνολο τιμών της h είναι το![\displaystyle \left[\frac{e+1}{e}+\frac{1}{e-1}-3,h\left(p \right) \right] \displaystyle \left[\frac{e+1}{e}+\frac{1}{e-1}-3,h\left(p \right) \right]](/forum/ext/geomar/texintegr/latexrender/pictures/11d1378dbd4ba908d102509c11cb3d28.png)
Ισχύει

ομόσημο του
Παίρνουμε το τριώνυμο

Είναι και παίρνοντας το τριώνυμο
και παίρνοντας το τριώνυμο  βρίσκουμε ρίζες
βρίσκουμε ρίζες  και
και  Όμως
Όμως  οπότε το
οπότε το  βρίσκεται εκτός των ριζών του
βρίσκεται εκτός των ριζών του  και άρα
και άρα 
Άρα ομόσημο του συντελεστή
ομόσημο του συντελεστή  του
του  και άρα
και άρα 
Γράφοντας
παίρνουμε
Αλλά επειδή η
επειδή η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο  και
και  και από την
και από την  έχουμε τελειώσει.
έχουμε τελειώσει.
Υ.Γ Αυτά όλα είναι λίγο γραψιματάκι κι όμως τα πληκτρολόγησα σε 100 χρόνια από το Mathtype γιατί το latex κολλούσε. Η LATEX μου έβγαλε την πίστη.
Γ1
Κοντά στο

Κοντά στο

από εδώ έχουμε τη συνέχεια στο μηδέν και επειδή κοντά στο
 απορρίπτεται η παραγωγισιμότητα στο μηδέν.
απορρίπτεται η παραγωγισιμότητα στο μηδέν.Γ2
Από τη συνέχεια της συνάρτησης στο σύνολο των αρνητικών ως γινόμενο εκθετικής και ημιτονοειδούς και από τη συνέχεια της συνάρτησης στο σύνολο των θετικών πραγματικών ως τετραγωνική ρίζα πολυωνυμικής και άρα συνεχούς συνάρτησης, λόγω της συνέχειάς της και στο μηδέν, θα είναι συνεχής στους πραγματικούς αριθμούς. Άρα η γραφική της παράσταση δεν έχει κατακόρυφες ασύμπτωτες.
Στέλνοντας

Άρα ο άξονας των τετμημένων είναι οριζόντια ασύμπτωτη της γραφικής παράστασης στο μείον άπειρο, οπότε δεν γίνεται να έχει και πλάγια ασύμπτωτη στο μείον άπειρο.
Στέλνοντας

Στέλνοντας

λόγω του Κανόνα De L' Hospital.
Οπότε πλάγια ασύμπτωτη στο συν άπειρο η
 και δεν έχει οριζόντια ασύμπτωτη στο συν άπειρο.
και δεν έχει οριζόντια ασύμπτωτη στο συν άπειρο.Γ3 Κάντε έναν Bolazno είναι κλασική άσκηση.
Γ4. η συνάρτηση f είναι μη παραγωγίσιμη στο 0 οπότε μόνο την χρονική στιγμή 0 δεν ορίζεται ρυθμός μεταβολής των τεταγμένων του σημείου

Για τα θετικά t

Αλλιώς το Δ4

Από εδώ έχουμε ότι είναι κυρτή η προς ολοκλήρωση συνάρτηση.
Για κάθε x,y στο [1,e] ισχύει
 με ισότητα μόνο όταν x=y
με ισότητα μόνο όταν x=yΑπό εδώ
![\displaystyle \int_{1}^{e}F\left( x \right)dx> \int_{1}^{e}\left( y^{\ln y}-2y^{\ln y}\ln y+2y^{\ln y}\frac{\ln y}{y} x\right)dx=y^{\ln y}\left[\left( 1-2\ln y \right)x+x^{2}\frac{\ln y}{y} \right]^{e}_{1}= \displaystyle \int_{1}^{e}F\left( x \right)dx> \int_{1}^{e}\left( y^{\ln y}-2y^{\ln y}\ln y+2y^{\ln y}\frac{\ln y}{y} x\right)dx=y^{\ln y}\left[\left( 1-2\ln y \right)x+x^{2}\frac{\ln y}{y} \right]^{e}_{1}=](/forum/ext/geomar/texintegr/latexrender/pictures/d167bbb03df00dd0b0a643347daa0a8e.png)
![\displaystyle =y^{\ln y}\left[ \left( e-1 \right)\left( 1-2\ln y \right)+\left( e-1 \right)\left( e+1 \right)\frac{\ln y}{y} \right]=\left( e-1 \right)y^{\ln y}\left( 1-2\ln y+\left( e+1 \right) \frac{\ln y}{y}\right) \displaystyle =y^{\ln y}\left[ \left( e-1 \right)\left( 1-2\ln y \right)+\left( e-1 \right)\left( e+1 \right)\frac{\ln y}{y} \right]=\left( e-1 \right)y^{\ln y}\left( 1-2\ln y+\left( e+1 \right) \frac{\ln y}{y}\right)](/forum/ext/geomar/texintegr/latexrender/pictures/7e21301fb5e7c50f71e91b0289613e5f.png)
Θεωρούμε τη συνάρτηση
 ορισμένη στο [1,e]
ορισμένη στο [1,e]Η h είναι παραγωγίσιμη στο [1,e] με

που είναι ομόσημη του

Παίρνουμε την
 στο [1,e] που με παραγώγους είναι άμεσο ότι είναι γνησίως φθίνουσα. Είναι όμως και συνεχής οπότε
στο [1,e] που με παραγώγους είναι άμεσο ότι είναι γνησίως φθίνουσα. Είναι όμως και συνεχής οπότε ![w\left([1,e]\right)=\left[w\left( e \right),w\left( 1\right)\right]=\left[ -2e,e-1 \right] w\left([1,e]\right)=\left[w\left( e \right),w\left( 1\right)\right]=\left[ -2e,e-1 \right]](/forum/ext/geomar/texintegr/latexrender/pictures/f78b8adddb807493e9b59b2e8643cef3.png) οπότε έχει ρίζα μάλιστα μοναδική λόγω γνήσιας μονοτονίας έστω
οπότε έχει ρίζα μάλιστα μοναδική λόγω γνήσιας μονοτονίας έστω 
Στο [1,ρ) ισχύει

Στο (ρ,e] ισχύει

και με
 συνεχή στο
συνεχή στο  η h είναι γνησίως αύξουσα στο [1,ρ] και γνησίως φθίνουσα στο [ρ,e] και επειδή είναι συνεχής ισχύει
η h είναι γνησίως αύξουσα στο [1,ρ] και γνησίως φθίνουσα στο [ρ,e] και επειδή είναι συνεχής ισχύει ![\displaystyle h\left( \left[ 1,p \right] \right)=\left[ h\left( 1 \right),h\left( p \right) \right]=\left[\frac{1}{e-1}-1,h\left(p \right) \right] \displaystyle h\left( \left[ 1,p \right] \right)=\left[ h\left( 1 \right),h\left( p \right) \right]=\left[\frac{1}{e-1}-1,h\left(p \right) \right]](/forum/ext/geomar/texintegr/latexrender/pictures/0a1c1b385e7b654706b19784caf7d21e.png) και
και ![\displaystyle h\left( \left[ p,e \right] \right)=\left[ h\left( e \right),h\left( p \right) \right]=\left[ \frac{e+1}{e}+\frac{1}{e-1}-3,h\left( p \right) \right] \displaystyle h\left( \left[ p,e \right] \right)=\left[ h\left( e \right),h\left( p \right) \right]=\left[ \frac{e+1}{e}+\frac{1}{e-1}-3,h\left( p \right) \right]](/forum/ext/geomar/texintegr/latexrender/pictures/adb59eea81fe2ec79f2385b04cdd1cfd.png)
Άρα το σύνολο τιμών της h είναι το
![\displaystyle \left[\frac{e+1}{e}+\frac{1}{e-1}-3,h\left(p \right) \right] \displaystyle \left[\frac{e+1}{e}+\frac{1}{e-1}-3,h\left(p \right) \right]](/forum/ext/geomar/texintegr/latexrender/pictures/11d1378dbd4ba908d102509c11cb3d28.png)
Ισχύει


ομόσημο του

Παίρνουμε το τριώνυμο


Είναι
 και παίρνοντας το τριώνυμο
και παίρνοντας το τριώνυμο  βρίσκουμε ρίζες
βρίσκουμε ρίζες  και
και  Όμως
Όμως  οπότε το
οπότε το  βρίσκεται εκτός των ριζών του
βρίσκεται εκτός των ριζών του  και άρα
και άρα 
Άρα
 ομόσημο του συντελεστή
ομόσημο του συντελεστή  του
του  και άρα
και άρα 
Γράφοντας

παίρνουμε

Αλλά
 επειδή η
επειδή η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο  και
και  και από την
και από την  έχουμε τελειώσει.
έχουμε τελειώσει.Υ.Γ Αυτά όλα είναι λίγο γραψιματάκι κι όμως τα πληκτρολόγησα σε 100 χρόνια από το Mathtype γιατί το latex κολλούσε. Η LATEX μου έβγαλε την πίστη.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες

 δεν πρέπει να εξεταστεί;
δεν πρέπει να εξεταστεί;