1.Είναι γνωστό ότι τα

είναι ομοκωνικά.
Έστω

και κυκλικά τα

.
Από Πάππο (ή

) στο

τα

είναι συνευθειακά,οπότε οι πολικές τους είναι συντρέχουσες που δίνει το ζητούμενο.
4.Έστω

.
Από

στο

τα

είναι συνευθειακά.Ομοίως και τα

είναι συνευθειακά.
Από

στο

τα

είναι συνευθειακά (και τα κυκλικά τους) ,από

στο

τα

είναι συνευθειακά,το οποίο δίνει το ζητούμενο (

στα

).
3.Έστω

.Από Πάππο στις

τα

είναι συνευθειακά.Ομοίως και τα

είναι συνευθειακά.Επομένως αρκεί τα

να βγουν προοπτικά.Αφού (βλ. παραπάνω) τα

είναι συνευθειακά (και τα κυκλικά τους) έπεται από

πως τα

είναι προοπτικά,δηλαδή οι

είναι συντρέχουσες,έστω στο

.Ανάλογα ορίζονται και τα

.
Από

στο

παίρνουμε πως τα

είναι συνευθειακά που δίνει το ζητούμενο.
2.Νομίζω το πιο ενδιαφέρον.
Αφήνουμε τις

να τμήσουν την

στα

και κυκλικά ορίζουμε τα

και

στις

αντίστοιχα.
Το κλειδί είναι ότι τα ζεύγη αυτά είναι ισοτομικά στις πλευρές τους.
Αυτό το δείχνουμε για τα

-και ομοίως η πρόταση έπεται και για τα άλλα ζεύγη.
Από

στο

και την ευθεία

,τα μέλη της οικογένειας κωνικών των παραπάνω σημείων τέμνουν την

σε συζυγή σημεία ενέλιξης-η οποία δεν είναι άλλη από την ισοτομικότητα.
Εμείς θέμε να δείξουμε ότι και οι

τέμνουν την

σε συζυγή σημεία της ίδιας ενέλιξης.Από το Δυικό του

,οι

είναι συζυγείς σε ενέλιξη.Προβάλλοντας τις ακτίνες αυτές στην

και επειδή έχουμε την ισοτομικότητα των

αρκεί να δείξουμε ότι τα

είναι ισοτομικά καθώς μια ενέλιξη καθορίζεται από δύο ζεύγη σημείων.Αυτό όμως ισχύει:Από προηγούμενο ερώτημα τα

είναι συνευθειακά,οπότε από Δυικό του

στο

με κέντρο το

έπεται η ισοτομικότητα.
Πλέον,αν

και

τα κυκλικά τους,τα αντίστοιχα ζεύγη είναι ισοτομικά στις πλευρές του
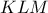
.Επομένως τα παραπάνω σημεία είναι ομοκωνικά και με ένα

λαμβάνουμε πως τα

είναι συνευθειακά,γεγονός που δείχνει την προοπτικότητα που θέλαμε.
Edit:καλύτερο τελείωμα
Edit2:Τυπογραφικά.Ευχαριστώ τον Πρόδρομο
 τα ζεύγη ισοτομικών σημείων ως προς τις πλευρές
τα ζεύγη ισοτομικών σημείων ως προς τις πλευρές  τριγώνου
τριγώνου  αντίστοιχα και ας είναι
αντίστοιχα και ας είναι  . Να δειχθεί ότι:
. Να δειχθεί ότι:  διέρχονται από το ίδιο σημείο (έστω
διέρχονται από το ίδιο σημείο (έστω  )
) διέρχονται από το ίδιο σημείο (έστω
διέρχονται από το ίδιο σημείο (έστω  ), με
), με 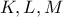 τα μέσ των πλευρών
τα μέσ των πλευρών  του τριγώνου
του τριγώνου  αντίστοιχα.
αντίστοιχα.  διέρχονται από το ίδιο σημείο (έστω
διέρχονται από το ίδιο σημείο (έστω  ) , με
) , με  .
. διέρχονται από το ίδιο σημείο (έστω
διέρχονται από το ίδιο σημείο (έστω  )
)
 παίρνω
παίρνω  .
. διατέμνουσας
διατέμνουσας  παίρνω
παίρνω  οπότε αντικαθιστώντας στην προηγούμενη προκύπτει
οπότε αντικαθιστώντας στην προηγούμενη προκύπτει  .
. (η μάλλον εναλλάσσοντας στην
(η μάλλον εναλλάσσοντας στην  τα
τα  για να τελειώνουμε
για να τελειώνουμε  και
και  .
. με πολλαπλασιασμό μας δίνουν από το τριγωνομετρικό
με πολλαπλασιασμό μας δίνουν από το τριγωνομετρικό  το ζητούμενο.
το ζητούμενο. είναι ομοκωνικά.
είναι ομοκωνικά. και κυκλικά τα
και κυκλικά τα  .
. ) στο
) στο  τα
τα  είναι συνευθειακά,οπότε οι πολικές τους είναι συντρέχουσες που δίνει το ζητούμενο.
είναι συνευθειακά,οπότε οι πολικές τους είναι συντρέχουσες που δίνει το ζητούμενο. .
. τα
τα  είναι συνευθειακά.Ομοίως και τα
είναι συνευθειακά.Ομοίως και τα  είναι συνευθειακά.
είναι συνευθειακά. τα
τα  είναι συνευθειακά (και τα κυκλικά τους) ,από
είναι συνευθειακά (και τα κυκλικά τους) ,από  τα
τα  είναι συνευθειακά,το οποίο δίνει το ζητούμενο (
είναι συνευθειακά,το οποίο δίνει το ζητούμενο ( στα
στα  ).
). .Από Πάππο στις
.Από Πάππο στις  τα
τα  είναι συνευθειακά.Ομοίως και τα
είναι συνευθειακά.Ομοίως και τα  είναι συνευθειακά.Επομένως αρκεί τα
είναι συνευθειακά.Επομένως αρκεί τα  να βγουν προοπτικά.Αφού (βλ. παραπάνω) τα
να βγουν προοπτικά.Αφού (βλ. παραπάνω) τα  είναι συνευθειακά (και τα κυκλικά τους) έπεται από
είναι συνευθειακά (και τα κυκλικά τους) έπεται από  είναι προοπτικά,δηλαδή οι
είναι προοπτικά,δηλαδή οι  είναι συντρέχουσες,έστω στο
είναι συντρέχουσες,έστω στο  .Ανάλογα ορίζονται και τα
.Ανάλογα ορίζονται και τα  .
. είναι συνευθειακά που δίνει το ζητούμενο.
είναι συνευθειακά που δίνει το ζητούμενο. να τμήσουν την
να τμήσουν την  στα
στα  και κυκλικά ορίζουμε τα
και κυκλικά ορίζουμε τα  και
και  στις
στις  αντίστοιχα.
αντίστοιχα. -και ομοίως η πρόταση έπεται και για τα άλλα ζεύγη.
-και ομοίως η πρόταση έπεται και για τα άλλα ζεύγη. στο
στο  και την ευθεία
και την ευθεία  είναι συζυγείς σε ενέλιξη.Προβάλλοντας τις ακτίνες αυτές στην
είναι συζυγείς σε ενέλιξη.Προβάλλοντας τις ακτίνες αυτές στην  αρκεί να δείξουμε ότι τα
αρκεί να δείξουμε ότι τα  είναι ισοτομικά καθώς μια ενέλιξη καθορίζεται από δύο ζεύγη σημείων.Αυτό όμως ισχύει:Από προηγούμενο ερώτημα τα
είναι ισοτομικά καθώς μια ενέλιξη καθορίζεται από δύο ζεύγη σημείων.Αυτό όμως ισχύει:Από προηγούμενο ερώτημα τα  με κέντρο το
με κέντρο το  έπεται η ισοτομικότητα.
έπεται η ισοτομικότητα. και
και  τα κυκλικά τους,τα αντίστοιχα ζεύγη είναι ισοτομικά στις πλευρές του
τα κυκλικά τους,τα αντίστοιχα ζεύγη είναι ισοτομικά στις πλευρές του 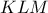 .Επομένως τα παραπάνω σημεία είναι ομοκωνικά και με ένα
.Επομένως τα παραπάνω σημεία είναι ομοκωνικά και με ένα  είναι συνευθειακά,γεγονός που δείχνει την προοπτικότητα που θέλαμε.
είναι συνευθειακά,γεγονός που δείχνει την προοπτικότητα που θέλαμε.