Δείξτε με ένα παράδειγμα ότι η αναπαραμέτρηση μιας κλειστής καμπύλης δεν είναι κατ'ανάγκη κλειστή.
Πώς μπορούμε να βρούμε μία τέτοια καμπύλη;
Πρέπει να βρούμε μια καμπύλη
 και την αναπαραμέτρησή της
και την αναπαραμέτρησή της  ώστε οι
ώστε οι  να μην είναι περιοδικές ;
να μην είναι περιοδικές ;Πώς όμως γίνεται λόγου χάρη η
 να είναι περιοδική, η
να είναι περιοδική, η  όμως όχι;
όμως όχι;
 μια κλειστής καμπύλης
μια κλειστής καμπύλης  οφείλει να είναι κλειστή από τον ορισμό της αλλαγής παραμέτρου
οφείλει να είναι κλειστή από τον ορισμό της αλλαγής παραμέτρου 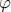 .
. 