Διαιρούν...

#1

Βρείτε όλα τα ζεύγη θετικών ακεραίων (a, b)

τέτοια ώστε $b| a^2, \ a | b^2, \ a + 1 | (b + 1)^2.$

#2

Επαναφορά!

Ορέστης Λιγνός · #3

socrates έγραψε: ↑
Παρ Φεβ 15, 2013 6:57 pm
Βρείτε όλα τα ζεύγη θετικών ακεραίων τέτοια ώστε $b| a^2, \ a | b^2, \ a + 1 | (b + 1)^2.$

Καλησπέρα σε όλους.

Αρχικά, είναι προφανές ότι όλα τα ζεύγη (a,b)=(m,m)

με

θετικό ακέραιο είναι λύσεις. Στο εξής, υποθέτουμε ότι $a \neq b$ .

Έστω (a,b)=d

. Παίρνουμε a=dx

και

με

. Οι πρώτες δύο διαιρετότητες δίνουν $y \mid dx^2$ και $x \mid dy^2$ , και αφού (x,y)=1

έχουμε ότι $xy \mid d$ . Έστω, d=xyk

με

θετικό ακέραιο.

Η τρίτη διαιρετότητα γράφεται $x^2yk+1 \mid x^2y^4k^2+2xy^2k+1$ . Είναι, $x^2y^4k \equiv -y^3k \pmod {x^2yk+1}$ , άρα $x^2yk+1 \mid 2xy^2k+1-y^3k$ , οπότε και $x^2yk+1 \mid x^2(2xy^2k+1-y^3k)=2x^3y^2k+x^2-x^2y^3k$ . Αφού $x^3y^2k \equiv -xy \pmod {x^2yk+1}$ και $x^2y^3k \equiv -y^2 \pmod {x^2yk+1}$ , προκύπτει ότι $x^2yk+1 \mid (x-y)^2,$ (1).

Επιπλέον, $x^2yk+1 \mid x^2k(y^2-2xy+x^2)=x^2ky^2-2x^4ky+x^4k$ , οπότε όπως πριν προκύπτει ότι $x^2yk+1 \mid -y+2x+x^4k,$ (2).

Διακρίνουμε τρεις περιπτώσεις.

Περίπτωση 1: y-2x-x^4k>0

. Τότε,

, άτοπο.
Περίπτωση 2: y-2x-x^4k=0

. Τότε, αφού (x,y)=1

, έχουμε

και

. Εύκολα λοιπόν έχουμε την λύση (a,b)=(k(k+2),k(k+2)^2)

.
Περίπτωση 3: y-2x-x^4k<0

. Τότε, έχουμε:

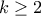$\bullet$ Αν $k \geq 2$ , τότε από την (1) προκύπτει ότι $y^2-(x^2k+2x)y+x^2-1 \geq 0$ . Επίσης από την (2) προκύπτει ότι $x^2yk+1 \leq 2x+x^4k-y \Rightarrow y \leq \dfrac{x^4k+2x-1}{x^2k+1} \leq x^2$ . Θεωρούμε το τριώνυμο f(y)=y^2-(x^2k+2x)y+x^2-1

, με παράγωγο f'(y)=2y-x^2k-2x

(εδώ έχουμε σταθεροποιήσει το

), η οποία για $y \leq x^2$ είναι αρνητική, καθώς
$f'(y) \leq 2x^2-x^2k-2x =(2-k)x^2-2x <0$ . Οπότε η

για $y \leq x^2$ φθίνει.

Επομένως, $0 \leq f(y) \leq f(1)=x^2-x^2k-2x <0$ , άτοπο.

$\bullet$ Αν k=1

, τότε η (1) γράφεται $x^2y+1 \mid y-2x-x^4$ . Διακρίνουμε δύο περιπτώσεις.

. Τότε, $y=\dfrac{x^4+2x-1}{x^2+1}$ , απ' όπου εύκολα έχουμε ότι x=1

, δηλαδή

.

$2x+x^4-y \geq 2(x^2y+1)$ . Τότε, $y \leq \frac{x^4+2x-2}{2x^2+1}$ . Τώρα θεωρούμε ξανά το τριώνυμο f(y)=y^2-(x^2+2x)y+x^2-1

με παράγωγο $f'(y)=2y-x^2-2x \leq \frac{2x^4+4x-8}{2x^2+1}-x^2-2x=\frac{2x^4+4x-8-(x^2+2x)(2x^2+1)}{2x^2+1}=\frac{2x-4x^3-x^2-8}{2x^2+1}<0$ , οπότε η

φθίνει για $y \leq \frac{x^4+2x-2}{2x^2+1}$ . Συνεπώς,

$0 \leq f(y) \leq f(1)=-2x<0$ , άτοπο.

Συνοψίζοντας λοιπόν, λύσεις τα ζεύγη (k,k)

και

με

θετικό ακέραιο.

Διαιρούν...

Διαιρούν...

Re: Διαιρούν...

Re: Διαιρούν...

Μέλη σε σύνδεση