Έστω
 ένας μεταθετικός δακτύλιος με μονάδα και
ένας μεταθετικός δακτύλιος με μονάδα και  με
με  αντιστρέψιμο.
αντιστρέψιμο. Θέλω να δείξω ότι η αντιστοιχία
 ορίζει ένα μοναδικό αυτομορφισμό του
ορίζει ένα μοναδικό αυτομορφισμό του ![R[x] R[x]](/forum/ext/geomar/texintegr/latexrender/pictures/c5b845aa2373916b6d15dbfe5ce5aae3.png) που είναι ταυτοτικός στο
που είναι ταυτοτικός στο  .
. Τι σημαίνει να είναι ταυτοτικός στο
 ;
;Συντονιστής: Demetres
 ένας μεταθετικός δακτύλιος με μονάδα και
ένας μεταθετικός δακτύλιος με μονάδα και  με
με  αντιστρέψιμο.
αντιστρέψιμο.  ορίζει ένα μοναδικό αυτομορφισμό του
ορίζει ένα μοναδικό αυτομορφισμό του ![R[x] R[x]](/forum/ext/geomar/texintegr/latexrender/pictures/c5b845aa2373916b6d15dbfe5ce5aae3.png) που είναι ταυτοτικός στο
που είναι ταυτοτικός στο  .
.  ;
;![R[x] R[x]](/forum/ext/geomar/texintegr/latexrender/pictures/c5b845aa2373916b6d15dbfe5ce5aae3.png) που είναι ταυτοτικός στο
που είναι ταυτοτικός στο  , πρέπει να δείξουμε ότι η αντιστοιχία είναι ισομορφισμός;
, πρέπει να δείξουμε ότι η αντιστοιχία είναι ισομορφισμός;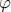 το πολυώνυμο
το πολυώνυμο  η απεικόνιση, ας την πούμε
η απεικόνιση, ας την πούμε  , απεικονίζει κάθε πολυώνυμο
, απεικονίζει κάθε πολυώνυμο  στο πολυώνυμο
στο πολυώνυμο  . Δηλαδή
. Δηλαδή  . Προφανώς τα σταθερά πολυώνυμα απεικονίζονται στον ευατό τους (αυτό σημαίνει ταυτοτική στον δακτύλιο
. Προφανώς τα σταθερά πολυώνυμα απεικονίζονται στον ευατό τους (αυτό σημαίνει ταυτοτική στον δακτύλιο  ). Απομένει να αποδειχθεί ότι:
). Απομένει να αποδειχθεί ότι:


 υπάρχει πολυώνυμο
υπάρχει πολυώνυμο  ώστε
ώστε 
 είναι αντιστρέψιμο.
είναι αντιστρέψιμο.nsmavrogiannis έγραψε:Αν ονομάσουμετο πολυώνυμο
η απεικόνιση, ας την πούμε
, απεικονίζει κάθε πολυώνυμο
στο πολυώνυμο
. Δηλαδή
.Απομένει να αποδειχθεί ότι:
(αυτά για να βγεί ομομορφισμός)


nsmavrogiannis έγραψε:
(για το 1-1)
 , σωστά;
, σωστά;  ;
; nsmavrogiannis έγραψε:για κάθε πολυώνυμουπάρχει πολυώνυμο
ώστε
(για το επί). Εδώ θα χρησιμοποιηθεί η υπόθεση ότι τοείναι αντιστρέψιμο.
 ένα πολυώνυμο. Θέλουμε να δείξουμε ότι υπάρχει ένα πολυώνυμο
ένα πολυώνυμο. Θέλουμε να δείξουμε ότι υπάρχει ένα πολυώνυμο  έτσι ώστε
έτσι ώστε  .
.  και
και 


 ;
;Οι τελευταίες πράξεις δεν χρειάζονται:Ειρήνη 33 έγραψε:Έστω
και
Τότε

Είναι σωστό αυτό;
Έχουμε ότι

Πώς μπορούμε να δείξουμε ότι αυτό ισούται με;

nsmavrogiannis έγραψε:Οι τελευταίες πράξεις δεν χρειάζονται:
 ; Μπορείτε να μου το εξηγήσετε;
; Μπορείτε να μου το εξηγήσετε;Κάπου στο βιβλίο που χρησιμοποιείτε (αλήθεια ποιό;) θα πρέπει να υπάρχει η έννοια του ομομορφισμού αντικατάστασης ή εκτίμησης (χρησιμοποιώ τον όρο από την ελληνική έκδοση της άλγεβρας του Lang σελίδα 101, η ορολογία αλλάζει από βιβλίο σε βιβλίο). Ο ομομορφισμός αυτός εξηγεί ότι ακόμη και αν τα πολυώνυμα ορίζονται όχι ως συναρτήσεις αλλά ακολουθίες πάλι οι πράξεις τους συμπεριφέρονται όπως οι πράξεις των συναρτήσεων.Ειρήνη 33 έγραψε:nsmavrogiannis έγραψε:Οι τελευταίες πράξεις δεν χρειάζονται:
Γιατί ισχύει ότι; Μπορείτε να μου το εξηγήσετε;
nsmavrogiannis έγραψε:Κάπου στο βιβλίο που χρησιμοποιείτε (αλήθεια ποιό;) θα πρέπει να υπάρχει η έννοια του ομομορφισμού αντικατάστασης ή εκτίμησης (χρησιμοποιώ τον όρο από την ελληνική έκδοση της άλγεβρας του Lang σελίδα 101, η ορολογία αλλάζει από βιβλίο σε βιβλίο). Ο ομομορφισμός αυτός εξηγεί ότι ακόμη και αν τα πολυώνυμα ορίζονται όχι ως συναρτήσεις αλλά ακολουθίες πάλι οι πράξεις τους συμπεριφέρονται όπως οι πράξεις των συναρτήσεων.Ειρήνη 33 έγραψε:nsmavrogiannis έγραψε:Οι τελευταίες πράξεις δεν χρειάζονται:
Γιατί ισχύει ότι; Μπορείτε να μου το εξηγήσετε;
 είναι επί; Πώς μπορούμε να δείξουμε ότι για κάθε πολυώνυμο
είναι επί; Πώς μπορούμε να δείξουμε ότι για κάθε πολυώνυμο  υπάρχει πολυώνυμο
υπάρχει πολυώνυμο  ώστε
ώστε  ;
; είναι
είναι 
 άρα
άρα 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης