 , ο οποίος περιέχει ένα ιδεώδες
, ο οποίος περιέχει ένα ιδεώδες  έτσι ώστε ο δακτύλιος-πηλίκο
έτσι ώστε ο δακτύλιος-πηλίκο  να είναι μεταθετικός.
να είναι μεταθετικός.Συντονιστής: Demetres
 , ο οποίος περιέχει ένα ιδεώδες
, ο οποίος περιέχει ένα ιδεώδες  έτσι ώστε ο δακτύλιος-πηλίκο
έτσι ώστε ο δακτύλιος-πηλίκο  να είναι μεταθετικός.
να είναι μεταθετικός.
![R=\bigg\{\bigg(\begin{smallmatrix}
[{\rm{k}}]_2 & [{\rm{m}}]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [{\rm{n}}]_2
\end{smallmatrix}\bigg)\,\Big|\; {\rm{k,m,n}}\in\{0,1\}\bigg\} R=\bigg\{\bigg(\begin{smallmatrix}
[{\rm{k}}]_2 & [{\rm{m}}]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [{\rm{n}}]_2
\end{smallmatrix}\bigg)\,\Big|\; {\rm{k,m,n}}\in\{0,1\}\bigg\}](/forum/ext/geomar/texintegr/latexrender/pictures/3013895add9fa38783a713a5e3edf7dc.png)
![\begin{aligned}
\bigg(\begin{smallmatrix}
[{\rm{k}}]_2 & [{\rm{m}}]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [{\rm{n}}]_2
\end{smallmatrix}\bigg)-\bigg(\begin{smallmatrix}
[{\rm{a}}]_2 & [{\rm{b}}]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [{\rm{c}}]_2
\end{smallmatrix}\bigg)&=\bigg(\begin{smallmatrix}
[{\rm{k}}]_2+[{\rm{a}}]_2 & [{\rm{m}}]_2+[{\rm{b}}]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [{\rm{n}}]_2+[{\rm{c}}]_2
\end{smallmatrix}\bigg)\in R\,,\\\noalign{\vspace{0.1cm}}
\bigg(\begin{smallmatrix}
[{\rm{k}}]_2 & [{\rm{m}}]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [{\rm{n}}]_2
\end{smallmatrix}\bigg)\,\bigg(\begin{smallmatrix}
[{\rm{a}}]_2 & [{\rm{b}}]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [{\rm{c}}]_2
\end{smallmatrix}\bigg)&=\bigg(\begin{smallmatrix}
[{\rm{ka}}]_2 & [{\rm{mc}}]_2+[{\rm{mc}}]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [{\rm{nc}}]_2
\end{smallmatrix}\bigg)\in R\,,\\\noalign{\vspace{0.1cm}}
\bigg(\begin{smallmatrix}
[1]_2 & [1]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [1]_2
\end{smallmatrix}\bigg)\,\bigg(\begin{smallmatrix}
[0]_2 & [1]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [1]_2
\end{smallmatrix}\bigg)=\bigg(\begin{smallmatrix}
[0]_2 & [0]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [1]_2
\end{smallmatrix}\bigg)&\neq\bigg(\begin{smallmatrix}
[0]_2 & [1]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [1]_2
\end{smallmatrix}\bigg)=\bigg(\begin{smallmatrix}
[0]_2 & [1]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [1]_2
\end{smallmatrix}\bigg)\,\bigg(\begin{smallmatrix}
[1]_2 & [1]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [1]_2
\end{smallmatrix}\bigg) \,.
\end{aligned} \begin{aligned}
\bigg(\begin{smallmatrix}
[{\rm{k}}]_2 & [{\rm{m}}]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [{\rm{n}}]_2
\end{smallmatrix}\bigg)-\bigg(\begin{smallmatrix}
[{\rm{a}}]_2 & [{\rm{b}}]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [{\rm{c}}]_2
\end{smallmatrix}\bigg)&=\bigg(\begin{smallmatrix}
[{\rm{k}}]_2+[{\rm{a}}]_2 & [{\rm{m}}]_2+[{\rm{b}}]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [{\rm{n}}]_2+[{\rm{c}}]_2
\end{smallmatrix}\bigg)\in R\,,\\\noalign{\vspace{0.1cm}}
\bigg(\begin{smallmatrix}
[{\rm{k}}]_2 & [{\rm{m}}]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [{\rm{n}}]_2
\end{smallmatrix}\bigg)\,\bigg(\begin{smallmatrix}
[{\rm{a}}]_2 & [{\rm{b}}]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [{\rm{c}}]_2
\end{smallmatrix}\bigg)&=\bigg(\begin{smallmatrix}
[{\rm{ka}}]_2 & [{\rm{mc}}]_2+[{\rm{mc}}]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [{\rm{nc}}]_2
\end{smallmatrix}\bigg)\in R\,,\\\noalign{\vspace{0.1cm}}
\bigg(\begin{smallmatrix}
[1]_2 & [1]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [1]_2
\end{smallmatrix}\bigg)\,\bigg(\begin{smallmatrix}
[0]_2 & [1]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [1]_2
\end{smallmatrix}\bigg)=\bigg(\begin{smallmatrix}
[0]_2 & [0]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [1]_2
\end{smallmatrix}\bigg)&\neq\bigg(\begin{smallmatrix}
[0]_2 & [1]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [1]_2
\end{smallmatrix}\bigg)=\bigg(\begin{smallmatrix}
[0]_2 & [1]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [1]_2
\end{smallmatrix}\bigg)\,\bigg(\begin{smallmatrix}
[1]_2 & [1]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [1]_2
\end{smallmatrix}\bigg) \,.
\end{aligned}](/forum/ext/geomar/texintegr/latexrender/pictures/7af1980b7728e114759547bfeb5a0519.png)
 είναι μη-μεταθετικός δακτύλιος με
είναι μη-μεταθετικός δακτύλιος με  στοιχεία. Για τον υποδακτύλιο
στοιχεία. Για τον υποδακτύλιο![I=\bigg\{\bigg(\begin{smallmatrix}
[0]_2 & [{\rm{r}}]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [{\rm{s}}]_2
\end{smallmatrix}\bigg)\,\Big|\; {\rm{r,s}}\in\{0,1\}\bigg\} I=\bigg\{\bigg(\begin{smallmatrix}
[0]_2 & [{\rm{r}}]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [{\rm{s}}]_2
\end{smallmatrix}\bigg)\,\Big|\; {\rm{r,s}}\in\{0,1\}\bigg\}](/forum/ext/geomar/texintegr/latexrender/pictures/3233c01482e5dff68a5a7328015c6456.png)
 και για κάθε
και για κάθε ![\bigg(\begin{smallmatrix}
[{\rm{k}}]_2 & [{\rm{m}}]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [{\rm{n}}]_2
\end{smallmatrix}\bigg)\in R\,,\; \bigg(\begin{smallmatrix}
[0]_2 & [{\rm{r}}]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [{\rm{s}}]_2
\end{smallmatrix}\bigg)\in I \bigg(\begin{smallmatrix}
[{\rm{k}}]_2 & [{\rm{m}}]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [{\rm{n}}]_2
\end{smallmatrix}\bigg)\in R\,,\; \bigg(\begin{smallmatrix}
[0]_2 & [{\rm{r}}]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [{\rm{s}}]_2
\end{smallmatrix}\bigg)\in I](/forum/ext/geomar/texintegr/latexrender/pictures/3293b0c4f918cd91ce472416212faee8.png) , ισχύουν
, ισχύουν![\begin{aligned}
\bigg(\begin{smallmatrix}
[{\rm{k}}]_2 & [{\rm{m}}]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [{\rm{n}}]_2
\end{smallmatrix}\bigg)\,\bigg(\begin{smallmatrix}
[0]_2 & [{\rm{r}}]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [{\rm{s}}]_2
\end{smallmatrix}\bigg)&=\bigg(\begin{smallmatrix}
[0]_2 & [{\rm{kr}}]_2+[{\rm{ms}}]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [{\rm{ns}}]_2
\end{smallmatrix}\bigg)\in I\,,\\\noalign{\vspace{0.1cm}}
\bigg(\begin{smallmatrix}
[0]_2 & [{\rm{r}}]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [{\rm{s}}]_2
\end{smallmatrix}\bigg)\,\bigg(\begin{smallmatrix}
[{\rm{k}}]_2 & [{\rm{m}}]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [{\rm{n}}]_2
\end{smallmatrix}\bigg)&=\bigg(\begin{smallmatrix}
[0]_2 & [{\rm{rn}}]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [{\rm{ns}}]_2
\end{smallmatrix}\bigg)\in I\,.
\end{aligned} \begin{aligned}
\bigg(\begin{smallmatrix}
[{\rm{k}}]_2 & [{\rm{m}}]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [{\rm{n}}]_2
\end{smallmatrix}\bigg)\,\bigg(\begin{smallmatrix}
[0]_2 & [{\rm{r}}]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [{\rm{s}}]_2
\end{smallmatrix}\bigg)&=\bigg(\begin{smallmatrix}
[0]_2 & [{\rm{kr}}]_2+[{\rm{ms}}]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [{\rm{ns}}]_2
\end{smallmatrix}\bigg)\in I\,,\\\noalign{\vspace{0.1cm}}
\bigg(\begin{smallmatrix}
[0]_2 & [{\rm{r}}]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [{\rm{s}}]_2
\end{smallmatrix}\bigg)\,\bigg(\begin{smallmatrix}
[{\rm{k}}]_2 & [{\rm{m}}]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [{\rm{n}}]_2
\end{smallmatrix}\bigg)&=\bigg(\begin{smallmatrix}
[0]_2 & [{\rm{rn}}]_2\\\noalign{\vspace{0.1cm}}
[0]_2 & [{\rm{ns}}]_2
\end{smallmatrix}\bigg)\in I\,.
\end{aligned}](/forum/ext/geomar/texintegr/latexrender/pictures/51cf8e2393f7df828246df33ca510f76.png)
 είναι ιδεώδες με
είναι ιδεώδες με  στοιχεία. Ο δακτύλιος-πηλίκο
στοιχεία. Ο δακτύλιος-πηλίκο  έχει
έχει  στοιχεία και, επομένως, είναι ισόμορφος με τον
στοιχεία και, επομένως, είναι ισόμορφος με τον  , ο οποίος είναι μεταθετικός δακτύλιος.
, ο οποίος είναι μεταθετικός δακτύλιος.
 είναι ένα σώμα και
είναι ένα σώμα και  ο δακτύλιος των άνω τριγωνικών
ο δακτύλιος των άνω τριγωνικών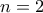 και
και  ) , τότε αυτός δεν
) , τότε αυτός δεν ώς πεπερασμένα παραγόμενη
ώς πεπερασμένα παραγόμενη  - άλγεβρα.
- άλγεβρα. είναι ημιαπλός δακτύλιος, όπου το
είναι ημιαπλός δακτύλιος, όπου το αποτελείται από τους άνω τριγωνικούς με μηδενικά στη διαγώνιο (Στο παράδειγμα του Γρηγόρη, είναι ακριβώς οι διαγώνιοι, δηλαδή 2 στοιχεία)
αποτελείται από τους άνω τριγωνικούς με μηδενικά στη διαγώνιο (Στο παράδειγμα του Γρηγόρη, είναι ακριβώς οι διαγώνιοι, δηλαδή 2 στοιχεία) ώς δακτύλιοι (άρα μεταθετικός)
ώς δακτύλιοι (άρα μεταθετικός) , είναι το μικρότερο που κάνει τον πηλικοδακτύλιο και ημιαπλό.
, είναι το μικρότερο που κάνει τον πηλικοδακτύλιο και ημιαπλό.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης