Προς το παρόν την χρησιμοποιήσαμε για να δώσουμε μία μορφή της Nullstellensatz του Hilbert για " πραγματικά κλειστά σώματα", (που δεν επιδέχονται γνήσια πραγματική επέκταση) όπως το $\mathbb{R}$, μαζί με τη συνηθισμένη με τα αλγεβρικά κλειστά σώματα (που δεν επιδέχονται γνήσια αλγεβρική επέκταση), ό...

Καλημέρα σε όλους μετά από πολύ καιρό. Θα ήθελα μία βοήθεια από τους αγγλομαθείς αλγεβριστές της ομάδας. Πρόσφατα, στο μάθημα της Αλγεβρικής Γεωμετρίας που παρακολουθώ, ήρθα σε επαφή με την έννοια του "anello reale" ("πραγματικός δακτύλιος") ως ενός δακτυλίου $R$ (αντιμεταθετικού με μονάδα) που ικαν...

Ευχαριστώ για τις λύσεις/προσεγγίσεις, βάζω και την δική μου λύση για πληρότητα. Θα αποδείξουμε ότι το $P_n$ έχει $n$ πραγματικές ρίζες. Χρησιμοποιούμε επαγωγή στο $n$. Για $n=1$, από τη διαφορική εξίσωση προκύπτει ότι ο σταθερός όρος είναι $0$, οπότε $P_1(x) = x$ (ισχύει). Παραγωγίζοντας τη διαφορι...

Το μονικό πολυώνυμο , βαθμού , ικανοποιεί την διαφορική εξίσωση



Να αποδειχθεί ότι το έχει όλες του τις ρίζες πραγματικές.

(Από φιλική ιταλική μαθηματική ομάδα).

Χρόνια πολλά στους εορτάζοντες, ιδιαίτερα στον Αλέξανδρο Συγκελάκη.

Νομίζω αν γράψουμε τη συνάρτηση ως



ξεπερνιούνται οι δυσκολίες.

Το πολυώνυμο γράφεται ως $(3a+1)(5b+1)(7c+3) - (7c+3)$. Θέτοντας $p$ οποιονδήποτε από τους (άπειρους, σύμφωνα με το γνωστό θεώρημα του Dirichlet) πρώτους της μορφής $7c+3$, έχουμε άπειρες επιλογές (πάντα σύμφωνα με το ίδιο θεώρημα) για τα $a, b$ έτσι ώστε οι $3a+1, 5b+1$ να είναι πρώτοι. Έτσι, $P(a,...

Λάμπρο, μια χαρά είναι η λύση σου. Απλά, στο αρχικό λήμμα, δεν μπαίνει το ολοκλήρωμα της περιοδικής συνάρτησης



αλλά η μέση τιμή της



Καλημέρα και συγχαρητήρια.

Στο ορθογώνιο τραπέζιο $STOK$ έχουμε $d^2 = 16 - (r-1)^2 = 15 + 2r - r^2$. Αν ισχύει $d=r$, τότε έχουμε την δευτεροβάθμια $2r^2 - 2r - 15 = 0$ με θετική λύση $\displaystyle r = \frac{1 + \sqrt{31}}{2}$. Ισχύει $OS^2 = d^2 + 1 = 16 + 2r - r^2$. Με νόμο συνημιτόνων στο $\triangle{OSK}$ έχουμε $\displa...

Καλησπέρα, συνεχίζουμε με τα θέματα των Invariants.

Να υπολογιστεί το

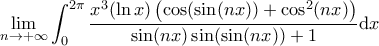
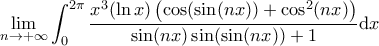
(Ελεγμένο, δεν υπάρχει τυπογραφικό!)

Τέλεια Κώστα.

Προσοχή Κώστα, υπάρχει λαθάκι ακριβώς στο τέλος. Μετά το δεν έχουμε (διορθώθηκε).

Καλησπέρα σε όλους, το παρόν από το Invariants Society του Πανεπιστημίου της Οξφόρδης. Για φυσικό $n \geqslant 2$ ορίζουμε το $f(n)$ ως τον μέγιστο πρώτο διαιρέτη του $n$. Έστω η ακολουθία $(a_n)_{n \in \mathbb{N}^*}$ με $a_1 = 2, \ \ a_{n+1} = a_n + f(a_n)$. Να βρεθεί ο μέγιστος $n$ με $a_n < 10^4$.

Καλημέρα Γιώργο και καλό υπόλοιπο καλοκαιριού. Έστω $L, l$ η μεγάλη και η μικρή πλευρά του ορθογωνίου. Στο σχήμα η γωνία $\angle{DAE} = 2 \pi / 3$, οπότε $DE = \sqrt{3} l$. Για τη μεγιστοποίηση του εμβαδού, έστω $\theta, \phi$ οι επίκεντρες γωνίες όπως φαίνονται στο σχήμα ($\theta + \phi = 2 \pi / 3...

Εύκολα αποδεικνύεται το Λήμμα: Για κάθε $A, B \in M_m (\mathbb{Z})$ και $n \in \mathbb{Z}$ ισχύει $\det(A+nB) \equiv \det(A) \mod n$. Λαμβάνοντας υπόψη την αντιμεταθετικότητα, η αρχική συνθήκη γράφεται ως $MN = 2019I$, όπου $M = A^2 + 2AB + 4B^2, \ N = A^2 - 2AB + 4B^2$. Έτσι, $M-N = 4 A B$ και, από...

Έστω οι θετικοί πραγματικοί $a_1,...,a_n$ με $n\geq 2$. Να εξετάσετε αν ισχύει η: $a_1^2+a_2^2+\cdots+a_n^2+a_1a_2\cdots a_n+2n-1\geq 3(a_1+a_2+\cdots+a_n)$ (Περιλαμβάνω το $0$ στις πιθανές τιμές των όρων χωρίς βλάβη, λόγω συνέχειας). Το μέρος της παράστασης που περιέχει τους όρους $a_1, a_2$ γράφε...

Η αρχική συνθήκη γράφεται $(P+I)(Q+I)=I \implies Q+I = (P+I)^{-1}$. Έχουμε $I + 2P + 3Q = 2(P+I) - 4I + 3(Q+I) = (Q+I) [ 2(P+I)^2 -4(P+I) + 3I]$. Οι πίνακες $P, Q$, ως μηδενοδύναμοι, έχουν μοναδική ιδιοτιμή το $0$. Άρα και οι $P+kI, Q + kI$ έχουν μοναδική ιδιοτιμή το $k$ και η ορίζουσα ισούται με (θ...

Για το πρώτο σκέλος μπορούμε εναλλακτικά να παρατηρήσουμε ότι η συνάρτηση έχει μοναδικό σημείο καμπής (από κυρτή σε κοίλη) και έτσι η παράσταση ελαχιστοποιείται για ισότητα των δύο μικρότερων από τα .

Παρατήρησε ότι χρησιμοποιείς συνεπαγωγές και όχι ισοδυναμίες. Το τελικό σου αποτέλεσμα λέει ότι το πρέπει να είναι περιττό, που διαφωνεί με το δεύτερο δεδομένο.

Ονομάζουμε $\displaystyle a_{k,n} \equiv \ln \left( 1 + \frac{1}{k} \right) - \sum_{i=1}^n \frac{1}{(k+1)i^{k+1}}$. Η οικογένεια ακολουθιών $(a_k)_n$ συγκλίνει μονότονα κατά σημείο στην $\displaystyle b_k \equiv \ln \left( 1 + \frac{1}{k} \right) - \frac{\zeta(k+1)}{k+1}$. Επίσης, για κάθε $n \in \m...