 , για κάθε μία από τις οποίες η εξίσωση
, για κάθε μία από τις οποίες η εξίσωση
έχει ακριβώς τέσσερεις ρίζες.
Συντονιστής: exdx
 , για κάθε μία από τις οποίες η εξίσωση
, για κάθε μία από τις οποίες η εξίσωση
ΓράφονταςAl.Koutsouridis έγραψε: ↑Δευ Απρ 17, 2023 6:58 pmΝα βρείτε όλες τις τιμές της παραμέτρου, για κάθε μία από τις οποίες η εξίσωση
έχει ακριβώς τέσσερεις ρίζες.
 , προκύπτει:
, προκύπτει:
 για οποιαδήποτε τιμή του
για οποιαδήποτε τιμή του  . Ακόμη, επειδή η
. Ακόμη, επειδή η  είναι συμμετρική ως προς τον
είναι συμμετρική ως προς τον  και:
και:
 (άλλωστε αν
(άλλωστε αν 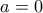 , η δοθείσα εξίσωση έχει 3 ακριβώς ρίζες).
, η δοθείσα εξίσωση έχει 3 ακριβώς ρίζες). :
:
 και ρίζες
και ρίζες  . Η θετική απορρίπτεται. Για να γίνει δεκτή η αρνητική, πρέπει:
. Η θετική απορρίπτεται. Για να γίνει δεκτή η αρνητική, πρέπει:
 :
:
 , μη αρνητική όταν
, μη αρνητική όταν  . Για κάθε μία από τις ρίζες τις εξίσωσης, βρίσκω τη συνθήκη που πρέπει να ικανοποιεί το
. Για κάθε μία από τις ρίζες τις εξίσωσης, βρίσκω τη συνθήκη που πρέπει να ικανοποιεί το  , ώστε η λύση να γίνει δεκτή.
, ώστε η λύση να γίνει δεκτή.

 :
:
 , μη αρνητική όταν
, μη αρνητική όταν  . Όμοια με παραπάνω:
. Όμοια με παραπάνω:

 η
η  έχει 4 ακριβώς διακριτές ρίζες, συνεπώς για το
έχει 4 ακριβώς διακριτές ρίζες, συνεπώς για το  ισχύει:
ισχύει:  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης